Question

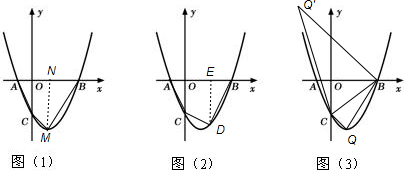
如图（1），抛物线y=x²-2x+k与x轴交于A、B两点，与y轴交于点C（0，-3）．      （注：图（2）、图（3）为解答备用图）
（1）求k值及A和B的坐标；
（2）设抛物线y=x²-2x+k与的顶点为M，求四边形ABMC的面积；
（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；
（4）在抛物线y=x²-2x+k与上求点Q，使△BCQ是以BC为直角边的直角三角形．

Answer 1

分析：（1）将C点坐标代入抛物线解析式可求k的值，由抛物线解析式求A，B两点坐标；
（2）根据A、B、M、N四点坐标，将四边形分割为两个三角形和一个梯形求面积；
（3）只要使△DBC面积最大即可，由此求D点坐标；
（4）分别过B，C两点作线段BC的垂线，交抛物线于Q点，求直线BQ或CQ的解析式，与抛物线解析式联立可求Q点坐标．

解答：解：（1）将C（0，-3）代入抛物线y=x²-2x+k中，得k=-3，
∴抛物线解析式为y=x²-2x-3，令y=0，得x=-1或3，
∴A（-1，0），B（3，0）；

（2）如图（1），过M点作MN⊥AB，垂足为N，由y=x²-2x-3=（x-1）²-4，可知M（1，-4），
∴S_{四边形ABMC}=S_△ACO+S_梯形OCMN+S_△BMN=

1

2

×1×3+

1

2

×（3+4）×1+

1

2

×（3-1）×4=9；

（3）存在，如图（2），设D（m，m²-2m-3），过D点作DE⊥AB，垂足为E，则
S_{四边形ABDC}=S_△ACO+S_梯形OCDE+S_△BDE
=

1

2

×1×3+

1

2

×[3-（m²-2m-3）]×m+

1

2

×（3-m）×[-（m²-2m-3）]
=-

3

2

m²+

9

2

m+6，
∵-

3

2

＜0，∴当m=-

9 2

-3

=

3

2

时，S_{四边形ABDC}最大，此时D（

3

2

，-

15

4

）；

（4）如图（3），∵B（3，0），C（0，-3），
∴△OBC为等腰直角三角形，
过B作线段BC的垂线，交抛物线于Q′点，则直线BQ′：y=-x+3，联立

y=-x+3 y=x2-2x-3

，
解得Q′（-2，5），
过C作线段BC的垂线，交抛物线于Q点，同理可得Q（1，-4）．
∴Q（1，-4）或（-2，5）．

点评：本题考查了二次函数的综合运用．关键是根据题意求抛物线解析式，将四边形分割为三角形与梯形的面积和求解，同时考查了坐标系中，线段的垂直关系．