题目内容
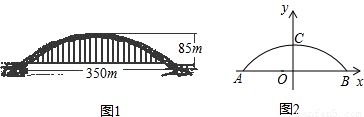
25、目前国内最大跨径的钢管混凝土拱桥--永和大桥,是南宁市又一标志性建筑,其拱形图形为抛物线的一部分(如图1),在正常情况下,位于水面上的桥拱跨度为350米,拱高为85米.
(1)在所给的直角坐标系中(如图2),假设抛物线的表达式为y=ax2+b,请你根据上述数据求出a,b的值,并写出抛物线的表达式;(不要求写自变量的取值范围,a,b的值保留两个有效数字)
(2)七月份汛期将要来临,当邕江水位上涨后,位于水面上的桥拱跨度将会减小,当水位上涨4m时,位于水面上的桥拱跨度有多大?(结果保留整数)

(1)在所给的直角坐标系中(如图2),假设抛物线的表达式为y=ax2+b,请你根据上述数据求出a,b的值,并写出抛物线的表达式;(不要求写自变量的取值范围,a,b的值保留两个有效数字)
(2)七月份汛期将要来临,当邕江水位上涨后,位于水面上的桥拱跨度将会减小,当水位上涨4m时,位于水面上的桥拱跨度有多大?(结果保留整数)

分析:(1)根据所建坐标系,易知A、B、C三点坐标,把A(或B)、C的坐标代入表达式求解;
(2)水位上涨4m,则求纵坐标为4时对应点的横坐标,根据对称性求水面宽即跨度.
(2)水位上涨4m,则求纵坐标为4时对应点的横坐标,根据对称性求水面宽即跨度.
解答:解:(1)∵桥拱高度OC=85m,即抛物线过点(0,85)
∴b=85又由已知得:AB=350m,即点A、B的坐标分别为(-175,0),(175,0)
则有0=1752•a+85
解得a≈-0.0028
所求抛物线的表达式为:y=-0.0028x2+85;
(2)设DE为水位上升4m后的桥拱跨度,
即当y=4时,有4=-0.0028x2+85
∴x≈±170 D(-170,0),E(170,0)

∴ED≈170+170=340(m)
答:当水位上涨4m时,位于水面上的桥拱跨度为340m.
∴b=85又由已知得:AB=350m,即点A、B的坐标分别为(-175,0),(175,0)
则有0=1752•a+85
解得a≈-0.0028
所求抛物线的表达式为:y=-0.0028x2+85;
(2)设DE为水位上升4m后的桥拱跨度,
即当y=4时,有4=-0.0028x2+85
∴x≈±170 D(-170,0),E(170,0)

∴ED≈170+170=340(m)
答:当水位上涨4m时,位于水面上的桥拱跨度为340m.
点评:此题运用数学建模思想把实际问题转化为数学模型,体现了数学的实用性,对激发学生学习数学的热情会有帮助.

练习册系列答案
相关题目