题目内容
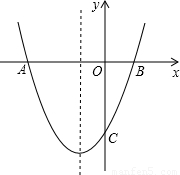
如图,已知知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,-3).(1)求抛物线的解析式;
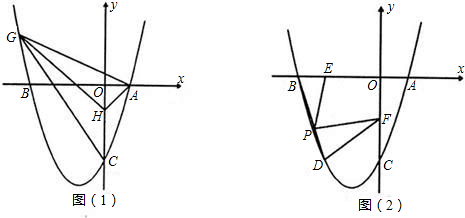
(2)如图(1),己知点H(0,-1).问在抛物线上是否存在点G (点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标;若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(-2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长.
分析:(1)由抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,-3),利用待定系数法即可求得二次函数的解析式;
(2)分别从GH∥AC与GH与AC不平行去分析,注意先求得直线GH的解析式,根据交点问题即可求得答案,小心不要漏解;
(3)利用待定系数法求得直线DF的解析式,即可证得△PBE∽△FDP,由相似三角形的对应边成比例,即可求得答案.
(2)分别从GH∥AC与GH与AC不平行去分析,注意先求得直线GH的解析式,根据交点问题即可求得答案,小心不要漏解;
(3)利用待定系数法求得直线DF的解析式,即可证得△PBE∽△FDP,由相似三角形的对应边成比例,即可求得答案.
解答: 解:(1)由题意得:
解:(1)由题意得:
,
解得:
,
∴抛物线的解析式为:y=x2+2x-3;
(2)解法一:
假设在抛物线上存在点G,设G(m,n),显然,当n=-3时,△HGC不存在.
①当n>-3时,
可得S△GHA=-
+
+
,S△GHC=-m,
∵S△GHC=S△GHA,
∴m+n+1=0,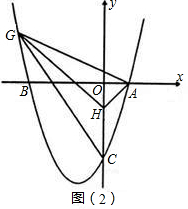
由
,
解得:
或
,
∵点G在y轴的左侧,
∴G(-
,
);
②当-4≤n<-3时,
可得S△GHA=
-
-
,S△GHC=-m,
∵S△GHC=S△GHA,
∴3m-n-1=0,
由
,
解得:
或
,
∵点G在y轴的左侧,
∴G(-1,-4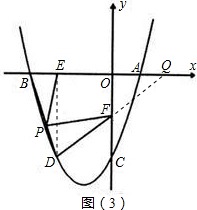 ).
).
∴存在点G(-
,
)或G(-1,-4).
解法二:
①如图①,当GH∥AC时,点A,点C到GH的距离相等,
∴S△GHC=S△GHA,
可得AC的解析式为y=3x-3,
∵GH∥AC,得GH的解析式为y=3x-1,
∴G(-1,-4);
②如图②,当GH与AC不平行时,
∵点A,C到直线GH的距离相等,
∴直线GH过线段AC的中点M(
,-
).
∴直线GH的解析式为y=-x-1,
∴G(-
,
),
∴存在点G(-
,
)或G(-1,-4).
(3)解法一:
如图③,∵E(-2,0),
∴D的横坐标为-2,
∵点D在抛物线上,
∴D(-2,-3),
∵F是OC中点,
∴F(0,-
),
∴直线DF的解析式为:y=
x-
,
则它与x轴交于点Q(2,0),
则QB=QD,得∠QBD=∠QDB,∠BPE+∠EPF+∠FPD=∠DFP+∠PDF+∠FPD=180°,
∵∠EPF=∠PDF,
∴∠BPE=∠DFP,
∴△PBE∽△FDP,
∴
=
,
得:PB•DP=
,
∵PB+DP=BD=
,
∴PB=
,
即P是BD的中点,
连接DE,
∴在Rt△DBE中,PE=
BD=
.
解法二:
可知四边形ABDC为等腰梯形,取BD的中点P′,
P′F=
(OB+CD)=
,
P′F∥CD∥AB,
连接EF,可知EF=DF=
,
即EF=FP′=FD,
即△FEP′相似△FP′D,
即∠EP′F=∠FP′D=∠FDP′,
即∠EP′F和∠EPF重合,
即P和P′重合,
P为BC中点,
PE=
BD=
(△BDE为直角三角形).
 解:(1)由题意得:
解:(1)由题意得:
|
解得:
|
∴抛物线的解析式为:y=x2+2x-3;
(2)解法一:
假设在抛物线上存在点G,设G(m,n),显然,当n=-3时,△HGC不存在.
①当n>-3时,
可得S△GHA=-
| m |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
∵S△GHC=S△GHA,
∴m+n+1=0,

由
|
解得:
|
|
∵点G在y轴的左侧,
∴G(-
3+
| ||
| 2 |
1+
| ||
| 2 |
②当-4≤n<-3时,
可得S△GHA=
| m |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
∵S△GHC=S△GHA,
∴3m-n-1=0,
由
|
解得:
|
|
∵点G在y轴的左侧,
∴G(-1,-4
 ).
).∴存在点G(-
3+
| ||
| 2 |
1+
| ||
| 2 |
解法二:
①如图①,当GH∥AC时,点A,点C到GH的距离相等,
∴S△GHC=S△GHA,
可得AC的解析式为y=3x-3,
∵GH∥AC,得GH的解析式为y=3x-1,
∴G(-1,-4);
②如图②,当GH与AC不平行时,
∵点A,C到直线GH的距离相等,
∴直线GH过线段AC的中点M(
| 1 |
| 2 |
| 3 |
| 2 |
∴直线GH的解析式为y=-x-1,
∴G(-
3+
| ||
| 2 |
1+
| ||
| 2 |
∴存在点G(-
3+
| ||
| 2 |
1+
| ||
| 2 |
(3)解法一:
如图③,∵E(-2,0),
∴D的横坐标为-2,
∵点D在抛物线上,
∴D(-2,-3),
∵F是OC中点,
∴F(0,-
| 3 |
| 2 |
∴直线DF的解析式为:y=
| 3 |
| 4 |
| 3 |
| 2 |
则它与x轴交于点Q(2,0),
则QB=QD,得∠QBD=∠QDB,∠BPE+∠EPF+∠FPD=∠DFP+∠PDF+∠FPD=180°,
∵∠EPF=∠PDF,
∴∠BPE=∠DFP,
∴△PBE∽△FDP,
∴
| PB |
| FD |
| BE |
| DP |
得:PB•DP=
| 5 |
| 2 |
∵PB+DP=BD=
| 10 |
∴PB=
| ||
| 2 |
即P是BD的中点,
连接DE,
∴在Rt△DBE中,PE=
| 1 |
| 2 |
| ||
| 2 |
解法二:
可知四边形ABDC为等腰梯形,取BD的中点P′,
P′F=
| 1 |
| 2 |
| 5 |
| 2 |
P′F∥CD∥AB,
连接EF,可知EF=DF=
| 5 |
| 2 |
即EF=FP′=FD,
即△FEP′相似△FP′D,
即∠EP′F=∠FP′D=∠FDP′,
即∠EP′F和∠EPF重合,
即P和P′重合,
P为BC中点,
PE=
| 1 |
| 2 |
| ||
| 2 |
点评:此题考查了待定系数法求二次函数的解析式,直线与二次函数的交点问题以及三角形面积问题的求解等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想、分类讨论思想与方程思想的应用

练习册系列答案
相关题目
 需写出解题步骤).
需写出解题步骤). (2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).
(2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0). 如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).
如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).