��Ŀ����
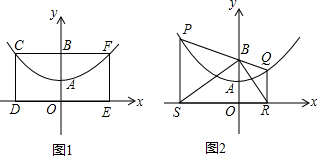
��ͼ1����֪�����ߵĶ���ΪA��0��1��������CDEF�Ķ���C��F���������ϣ���D��E��x���ϣ�CF��y���ڵ�B��0��2�����������Ϊ8����1���������ߵĽ���ʽ��
��2����ͼ2������PΪ�����������ϵ�һ���㣬���ж��Ե�PΪԲ�ģ�PBΪ�뾶��Բ��x���λ�ù�ϵ����˵�����ɣ�
��3����ͼ2�����P���������������A���غϣ�ֱ��PB�������ߵ���һ������ΪQ������P��Q�ֱ���x��Ĵ��ߣ�����ֱ�ΪN��M������PO��QO����֤����QMO�ס�PNO��

��������1���ȸ��ݵ�B��0��2����CF•OB=8����֪CF=4���ɾ��ε����ʿɵó�C��F������꣬���ô���ϵ����������������ߵĽ���ʽ��
��2����P���������x0��
x02+1�������������ľ��빫ʽ�ɵó�PB�ij����ٸ���P��x��ľ���Ϊ
x02+1���ɵó����ۣ�
��3���ɣ�2����֪��PB=PN��QB=QM���ٸ���PN��QM��ֱx��ɵó�QM��BO��PN����ƽ���߷��߶γɱ�����������QMO=��PNO=90�㼴�ɵó���QMO�ס�PNO��
��2����P���������x0��
| 1 |
| 4 |
| 1 |
| 4 |
��3���ɣ�2����֪��PB=PN��QB=QM���ٸ���PN��QM��ֱx��ɵó�QM��BO��PN����ƽ���߷��߶γɱ�����������QMO=��PNO=90�㼴�ɵó���QMO�ס�PNO��
����⣺��1���ߵ�B��0��2����
��OB=2��
�֡�CF•OB=8��
��CF=4��
�������֪����C��-2��2������F��2��2����
�������ߵĽ���ʽΪy=ax2+bx+c��
��
��
�������ߵĽ���ʽΪy=
x2+1��
��2����P���������x0��
x02+1����
��PB=
=
x02+1��
�ֵ�P��x��ľ���Ϊ
x02+1��
���Ե�PΪԲ�ġ�PBΪ�뾶��Բ��x�����У�
��3���ɣ�2����֪��PB=PN��QB=QM��
��PN��QM��ֱx�ᣬ
��QM��BO��PN��
��
=
��
��
=
��
�ߡ�QMO=��PNO=90�㣬
���QMO�ס�PNO��
��OB=2��
�֡�CF•OB=8��
��CF=4��
�������֪����C��-2��2������F��2��2����
�������ߵĽ���ʽΪy=ax2+bx+c��
��
|
�������ߵĽ���ʽΪy=
| 1 |
| 4 |
��2����P���������x0��
| 1 |
| 4 |
��PB=
x02+(
|
| 1 |
| 4 |
�ֵ�P��x��ľ���Ϊ
| 1 |
| 4 |
���Ե�PΪԲ�ġ�PBΪ�뾶��Բ��x�����У�
��3���ɣ�2����֪��PB=PN��QB=QM��
��PN��QM��ֱx�ᣬ
��QM��BO��PN��
��
| QB |
| BP |
| MO |
| ON |
��
| QM |
| PN |
| MO |
| NO |
�ߡ�QMO=��PNO=90�㣬
���QMO�ס�PNO��
���������⿼����Ƕ��κ����ۺ��⣬�漰������ϵ��������κ����Ľ���ʽ�������ľ��빫ʽ�����ߵ����ʡ�ƽ���ߵ��ж������ʡ����������ε��ж����漰��Ϲ㣬�ѶȽϴ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ���ϣ�CF��y���ڵ�B��0��2�����������Ϊ8��
���ϣ�CF��y���ڵ�B��0��2�����������Ϊ8��