题目内容
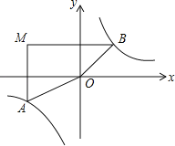
【题目】如图,已知平行四边形ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′若∠ADC=60°,∠ADA′=45°,则∠DA′E′=______度.

【答案】165°
【解析】
根据平行四边形的性质、三角形外角的性质和旋转的性质分别求出∠DA′B和∠B A′E′的度数即可.
解:∵∠ADC=60°,∠ADA′=45°,
∴∠A′DC=15°,∠DCB=120°,∠ABC=60°,
∴∠DA′B=∠A′DC+∠DCB=135°,
∵∠AEB=90°,
∴∠BAE=30°,
∴∠B A′E′=30°,
∴∠DA′E′= ∠DA′B+∠B A′E′=165°,
故答案为:165.

练习册系列答案
相关题目