题目内容
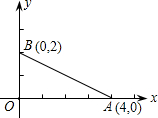如图，A（4，0）、B（0，2）是直角坐标系中的两点，点C在y轴上，若由点A、O、C为顶点组成的三角形与△AOB相似，则点C的坐标为________（填写满足条件的一点即可）．
（0，8）（答案不唯一）
分析：利用相似三角形对应边的比等于相似比求得线段OC的长即可求得点C的坐标．
解答：∵A（4，0）、B（0，2），
∴AO=4，BO=3，
∵由点A、O、C为顶点组成的三角形与△AOB相似，
∴
=
，
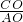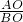即：
解得：CO=8，
∴点C的坐标为（0，8）
故答案为：（0，8）（答案不唯一）．
点评：本题考查了相似三角形的性质，解题的关键是将点的坐标转化为线段的长．
分析：利用相似三角形对应边的比等于相似比求得线段OC的长即可求得点C的坐标．
解答：∵A（4，0）、B（0，2），
∴AO=4，BO=3，
∵由点A、O、C为顶点组成的三角形与△AOB相似，
∴
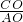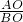=，即：
解得：CO=8，
∴点C的坐标为（0，8）
故答案为：（0，8）（答案不唯一）．
点评：本题考查了相似三角形的性质，解题的关键是将点的坐标转化为线段的长．
练习册系列答案
相关题目
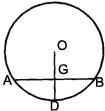14、如图，已知⊙P的半径OD=5，OD⊥AB，垂足是G，OG=3，则弦AB=
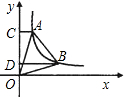如图，已知A，B两点是反比例函数y=
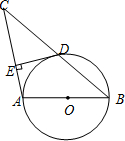如图AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC于点E．