题目内容
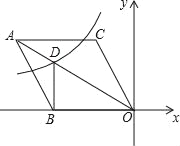
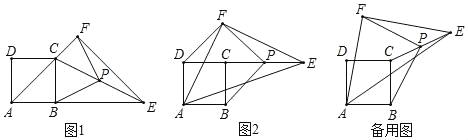
【题目】等腰Rt△AEF(其中FA=FE,∠AFE=90°,AE=6)与正方形ABCD(其中AB=2)有共同的顶点A,连接CE,点P是CE的中点,连接PB,PF.
(1)如图1,当点E恰好落在AB的延长线上时,请求出∠BPF的度数,并求出PB与PF的长.
(2)如图2,把等腰Rt△AEF绕点A旋转,当点E恰好在DC的延长线上时,
①请求出PC的长.
②判断PB与PF的数量关系与位置关系,并说明理由.
(3)把等腰Rt△AEF绕点A由如图1所示的位置逆时针旋转180°,在旋转过程中,点P的位置也随之改变,请思考点P运动的轨迹,直接写出点P运动的路程____.(结果保留π)
【答案】(1)∠FPB=90°;PF=![]() ;BP=
;BP=![]() ;(2)①CP=2
;(2)①CP=2![]() ﹣1;②PF⊥BP,PF=BP;(3)3π
﹣1;②PF⊥BP,PF=BP;(3)3π
【解析】
(1)根据勾股定理可求CE=2![]() ,根据直角三角形斜边上的中线等于斜边的一半,可求BP=PF=
,根据直角三角形斜边上的中线等于斜边的一半,可求BP=PF=![]() ,∠FPB=2∠FEA=90°;
,∠FPB=2∠FEA=90°;
(2)①由勾股定理可求DE的长,即可求CE的长,由P点是CE中点可求CP的长;
②过点E作GE∥BC,交BP的延长线于G,连接FG,BF,由题意可证△GEP≌△BCP,可得BP=GP,GE=BC,即可证△AFB≌△EFG,可得BF=FG,∠AFB=∠EFG,可得△BFG是等腰直角三角形,则PF⊥BP,PF=BP;
③以点A为原点,AB为x轴,AD为y轴建立直角坐标系,连接AC,BD交于点G.由题意可求点G(1,1),点C(2,2)设E(x,y),由AE=6,可得x2+y2=36,则可求点P(![]() ,
,![]() ),根据两点公式可求GP=3,即点P在以G为圆心,半径为3的圆上运动,即可求点P运动的路程.
),根据两点公式可求GP=3,即点P在以G为圆心,半径为3的圆上运动,即可求点P运动的路程.
解:(1)∵FA=FE,∠AFE=90°
∴∠FEA=45°
∵AB=2,AE=6
∴BE=4
在Rt△BCE中,CE=![]() =2
=2![]()
∵∠CFE=90°,点P是CE中点,
∴PE=PF=CP=![]() ,
,
∴∠PEF=∠PFE
即∠FPC=2∠FEP
∵∠CBE=90°,点P是CE中点
∴BP=PE=![]() ,
,
∴∠PEB=∠PBE
∴∠CPB=2∠PEB
∵∠FPB=∠FPC+∠CPB=2∠FEP+2∠PEB=2∠FEB
∴∠FPB=90°
(2)①∵AE=6,AD=2
∴由勾股定理可得:DE=![]() =4
=4![]() ,
,
∴CE=DE﹣DC=4![]() ﹣2
﹣2
∵点P是CE中点
∴CP=![]() =2
=2![]() ﹣1
﹣1
②过点E作GE∥BC,交BP的延长线于G,连接FG,BF,
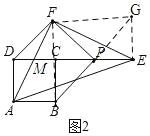
∵GE∥BC
∴∠BCE=∠GEP=90°且CP=PE,∠BPC=∠GPE
∴△GEP≌△BCP(AAS)
∴BP=GP,GE=BC
∵CD∥AB
∴∠FAB=∠FME
∵∠FME+∠FED=90°,∠FED+∠FEG=90°
∴∠FME=∠FEG
∴∠FAB=∠FEG,且GE=CB=AB,AF=EF
∴△AFB≌△EFG(SAS)
∴BF=FG,∠AFB=∠EFG
∵∠AFB+∠BFE=90°
∴∠BFE+∠EFG=90°
∴∠BFG=90°且BF=FG
∴△BFG是等腰直角三角形且BP=PG
∴PF⊥BP,PF=BP
(3)以点A为原点,AB为x轴,AD为y轴建立直角坐标系,连接AC,BD交于点G.
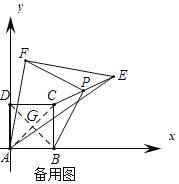
∵四边形ABCD是正方形,AB=2
∴AB=2=BC=CD=AD,AG=CG
∴点C(2,2)且点A(0,0)
∴点G(1,1)
设E(x,y)
∵AE=6
∴x2+y2=36
∵点P是CE的中点,且点C(2,2),点E(x,y)
∴点P(![]() ,
,![]() ),
),
∴GP=![]() =
=![]() =3
=3
∴点P运动的路程=![]() =3π
=3π
故答案为:3π

 阅读快车系列答案
阅读快车系列答案