题目内容
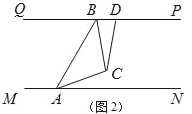
【题目】如图,已知△ABC是等边三角形,D是AB边上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.
(1)求证:CD=DE;

(2)若D是AB延长线上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.请画出图形,判断CD=DE是否还成立?若成立,请给予证明;若不成立,请说明理由.

【答案】(1)证明见解析;(2)成立,证明见解析.
【解析】
(1)过点D作DF//BC,交AC于F,由等边三角形的性质可得AF=AD,进而可得CF=BD,根据外角性质可知∠FCD+∠CDF=60°,由∠CDE=60°,∠ADF=60°可得∠CDF+∠EDB=60°,进而可得∠FCD=∠EDB,由BE是外角平分线可得∠CBE=60°,即可证明∠DBE=∠CFD=120°,即可证明△CFD≌△DEB,进而可得CD=DE;(2)过点D作DP//BC,交AC延长线于点P,由等边三角形及平行线性质可得CP=BD,根据外角性质可得∠PCD=∠A+∠ADC=60°+∠ADC,由∠BDE=∠CDE+∠ADC=60°+∠ADC可证明∠PCD=∠BDE,根据BE是外角平分线可得∠EBD=∠P=60°,即可证明△PCD≌△BDE,进而可得CD=DE.
(1)如图,过点D作DF//BC,交AC于F,
∵△ABC是等边三角形,DF//BC,
∴CF=BD,∠AFD=60°,
∴∠CFD=180°-60°=120°,
∵DE是外角平分线,
∴∠CBE=60°,
∴∠DBE=120°,
∴∠CFD=∠DBE,
∵∠FCD+∠CDF=∠AFD=60°,∠BDE+∠CDF=180°-∠ADF-∠CDE=180°-60°-60°=60°,
∴∠FCD=∠BDE,
∴△CFD≌△DEB,
∴CD=DE.

(2)过点D作DP//BC,交AC延长线于点P,
∵△ABC是等边三角形,DP//BC,
∴PC=BD,∠P=60°,
∵BE是外角平分线,
∴∠DBE=60°,
∴∠DBE=∠P,
∵∠PCD=∠A+∠ADC=60°+∠ADC,∠BDE=∠ADC+∠CDE=60°+∠ADC,
∴∠PCD=∠BDE,
∴△PCD≌△BDE,
∴CD=DE


 阅读快车系列答案
阅读快车系列答案