题目内容
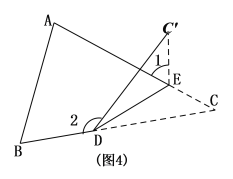
【题目】如图，将一张长方形的纸条ABCD沿EF折叠，AD交
于点G，若折叠后
(1)求∠CEF的度数；
(2)求证：△EFG是等腰三角形.
【答案】（1）∠CEF=66°；（2）证明见解析；
【解析】
（1）根据平行线性质可得∠BEC′=∠AGC′，由折叠的性质可得∠FEC′=∠CEF，根据平角的性质求出∠CEF的度数即可；（2）根据平行线性质可得∠EFG=∠FEC，根据折叠性质可得∠CEF=∠GEF，由等量代换可证明∠GEF=∠GFE，进而可得答案.
（1）∵AG//BE，∠AGC′=48°，
∴∠BEC′=∠AGC′=48°，
∵由折叠的性质得：∠FEC′=∠CEF，
∴∠CEF=
（180°-∠BEC′）=66°.
（2）∵DG//CE，
∴∠EFG=∠CEF，
∵∠CEF=∠GEF，
∴∠EFG=∠GEF，
∴EG=FG，
∴△EFG是等腰三角形.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
