题目内容
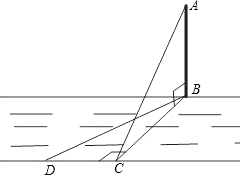 如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处测得塔顶仰角∠ACB=30°.
如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处测得塔顶仰角∠ACB=30°.(1)若河宽BC是60米,求塔AB的高;(精确到0.1米;参考数据:
| 2 |
| 3 |
(2)若河宽BC无法度量.则应如何测量塔AB的高度呢小明想出了另外一种方法:从点C出发,沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走a米到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高.
分析:根据题意构造直角三角形;本题涉及多个直角三角形,应利用其公共边构造相应的关系,进而可求出答案.
解答:解:(1)在Rt△ABC中,∠ACB=30°,BC=60.
∴AB=BC•tan∠ACB=60×
=20
≈34.6(米);
所以,塔AB的高约是34.6米.
(2)在Rt△BCD中,∠BDC=60°,CD=a.
∴BC=CD•tan∠BDC=
a.
又在Rt△ABC中,AB=BC•tan∠ACB=
a×
=a(米).
所以,塔AB的高为a米.
∴AB=BC•tan∠ACB=60×
| ||
| 3 |
| 3 |
所以,塔AB的高约是34.6米.
(2)在Rt△BCD中,∠BDC=60°,CD=a.
∴BC=CD•tan∠BDC=
| 3 |
又在Rt△ABC中,AB=BC•tan∠ACB=
| 3 |
| ||
| 3 |
所以,塔AB的高为a米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
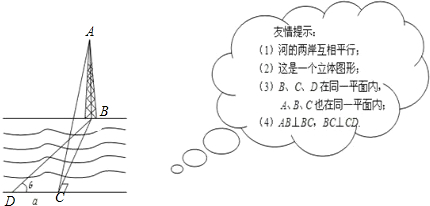
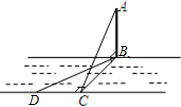 如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处,测得仰角∠ACB=30°.
如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处,测得仰角∠ACB=30°.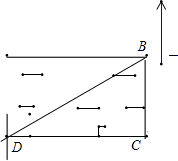 (2011•普宁市一模)如图,某学习小组为了测量河BC的宽度,在离C点20米处的D点测得B在北偏东60°的方向上(三角形BDC是直角三角形),求河BC的宽度(精确到0.1米)(供选
(2011•普宁市一模)如图,某学习小组为了测量河BC的宽度,在离C点20米处的D点测得B在北偏东60°的方向上(三角形BDC是直角三角形),求河BC的宽度(精确到0.1米)(供选