题目内容
边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为____.

试题考查知识点:正方形的性质,垂直平分线的判定与性质,三角形
思路分析:把所求的线段放在构建的特殊三角形内
具体解答过程:
如图所示。连接HC、DF,且HC与DF交于点P

∵正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG
∴∠BCF=∠DCG=30°,FC =DC,∠EFC=∠ADC=90°
∠BCG=∠BCD+∠DCG=90°+30°=120°
∠DCF=∠BCG-∠BCF-∠DCG=120°-30°-30°=60°
∴△DCF是等边三角形,∠DFC=∠FDC=60°
∴∠EFD=∠ADF=30°,HF=HD
∴HC是FD的垂直平分线,∠FCH=∠DCH= ∠DCF=30°
∠DCF=30°
在Rt△HDC中,HD=DC·tan∠DCH=
∵正方形ABCD的边长为3
∴HD=DC·tan∠DCH=3×tan30°=3× =
=
试题点评:构建新的三角形,利用已有的条件进行组合。
思路分析:把所求的线段放在构建的特殊三角形内
具体解答过程:
如图所示。连接HC、DF,且HC与DF交于点P

∵正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG
∴∠BCF=∠DCG=30°,FC =DC,∠EFC=∠ADC=90°
∠BCG=∠BCD+∠DCG=90°+30°=120°
∠DCF=∠BCG-∠BCF-∠DCG=120°-30°-30°=60°
∴△DCF是等边三角形,∠DFC=∠FDC=60°
∴∠EFD=∠ADF=30°,HF=HD
∴HC是FD的垂直平分线,∠FCH=∠DCH=
 ∠DCF=30°
∠DCF=30°在Rt△HDC中,HD=DC·tan∠DCH=

∵正方形ABCD的边长为3
∴HD=DC·tan∠DCH=3×tan30°=3×
 =
=
试题点评:构建新的三角形,利用已有的条件进行组合。

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目




 A =
A = ,则tan B=( )
,则tan B=( )



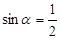 。
。 )
)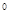 +(-1)
+(-1) 

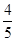



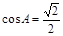 ,
, ,则这个三角形一定是……( )
,则这个三角形一定是……( ) km的C处.
km的C处.