题目内容
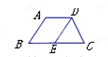
（10分）如图，四边形ABCD中，AB∥CD，AC平分∠BAD ，CE∥AD交AB于点E。
小题1:（1）判断：四边形AECD是什么形状？并给出理由。
小题2:（2）若点E是AB的中点，是判断△ABC的形状，并给出理由。
小题1:（1）判断：四边形AECD是什么形状？并给出理由。
小题2:（2）若点E是AB的中点，是判断△ABC的形状，并给出理由。
小题1:（1）菱形
小题2:（2）直角三角形
（1）∵AB∥CD，AD∥CE
∴AECD为平行四边形，∠ACD=∠CAE
又∵AC平分∠BAD得到∠CAD=∠CAE
∴∠ACD=∠CAD ∴AD=DC
又∵AECD为平行四边形
∴AECD为菱形
（2）E为AB中点则有AE=EB=EC
∴∠ECA=∠CAE，∠BCE=∠CBE
又∠ECA+∠CAE+∠BCE+∠CBE=180°
∴∠ECA+∠BCE=90°
∴△ABC为直角三角形
∴AECD为平行四边形，∠ACD=∠CAE
又∵AC平分∠BAD得到∠CAD=∠CAE
∴∠ACD=∠CAD ∴AD=DC
又∵AECD为平行四边形
∴AECD为菱形
（2）E为AB中点则有AE=EB=EC
∴∠ECA=∠CAE，∠BCE=∠CBE
又∠ECA+∠CAE+∠BCE+∠CBE=180°
∴∠ECA+∠BCE=90°
∴△ABC为直角三角形
练习册系列答案
阅读快车系列答案
相关题目
的坐标为
轴，
轴和原点）并写出点
的坐标；
为基本图形，利用轴对称或旋转或平移设计一个图案，说明你的创意
cm的速度运动，同时，点Q从点D出发沿DB方向以每秒1cm的速度运动，当点P到达点C时，P，Q同时停止运动，设运动的时间为x秒.
