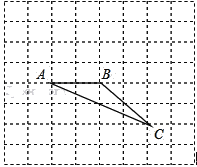
题目内容
【题目】如图所示,在矩形ABCD中,四个内角平分线相交于E、F, 若AB= 8cm,Ad=20cm,求EF的长度.
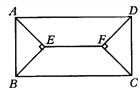
【答案】12cm
【解析】试题分析:延长BE交AD于M,延长DF交BC于N,根据矩形的性质求出∠DAE=∠BAE=∠ABE=∠CBE=45°,AD∥BC,AD=BC,求出AE⊥BM,AB=AM,得出平行四边形BMDN和平行四边形EFDM,即可求出EF=DM,求出DM即可.
试题解析:延长BE交AD于M,延长DF交BC于N,
∵四边形ABCD是矩形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,BC=AD= 20cm,AD∥BC,
∴∠AMB=∠CBM,
∵AE、BE分别平分∠DAB、∠ABC,∴∠DAE=∠BAE=45°,∠ABM=∠CBM=45°,
∴∠AMB=∠ABM=45°,∴AM=AB=8cm,
∴DM=20cm-8cm=12cm,同理BN=12cm,即DM=BN,DM∥BN,
∴四边形BMDN是平行四边形,
∴BM=DN,
∵∠ABM=∠BAE=45°,∴∠AEB=90°,即AE⊥BM,
∵AB=AM,∴BE=EM,
同理FN=DF,
∴EM=DF,
∵BM∥DN,
∴四边形MEFD是平行四边形,
∴EF=DM=12cm.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目