Question

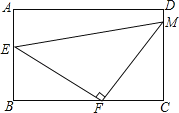
【题目】在矩形ABCD中，E、F、M分别为AB、BC、CD边上的点，且AB=6，BC=7，AE=3，DM=2，EF⊥FM，则EM的长为 ．

Answer 1

【答案】5．

【解析】

试题分析：由四边形ABCD是矩形，得到∠B=∠C=90°，CD=AB=6，根据AE=3，DM=2，于是得到BE=3，CM=4，推出△BEF∽△CFM，得到关于BF的比例式，进而可求出EM，EF的长，再利用勾股定理即可求出EM的长．

解：∵四边形ABCD是矩形，

∴∠B=∠C=90°，CD=AB=6，

∵AE=3，DM=2，

∴BE=3，CM=4，

∵EF⊥FM，

∴∠BEF+∠BFE=∠BFE+∠MFC=90°，

∴∠BEF=∠CFM，

∴△BEF∽△CFM，

∴，

∴，

解得：BF=3，或BF=4，

∴CF=4，或CF=3，

∴EF==5，FM==5，

∴EM==5，

故答案为：5．