题目内容
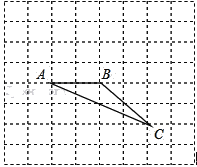
【题目】如图在8×8的正方形网格中，△ABC 的顶点在边长为1的小正方形的顶点上．
（1）填空：∠ABC= ，BC= ；
（2）若点A在网格所在的坐标平面里的坐标为（1，﹣2），请你在图中找出一点D，并作出以A、B、C、D四个点为顶点的平行四边形，求出满足条件的D点的坐标．
【答案】（1）135°，2
；（2）D1（3，-4）或D2（7，-4）或D3（-1，0）．
【解析】
（1）根据图形知道CB是一个等腰三角形的斜边，所以容易得出
的度数，利用勾股定理可以求出BC的长度；
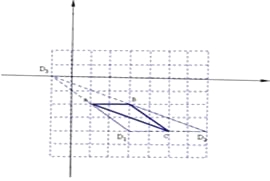
（2）根据A点的坐标（1，-2），并且ABCD为平行四边形，如图D的位置有三种情况．
解：（1）由图形可得：∠ABC=45°+90°=135°，BC=
；
故答案为：135°，2；
（2）满足条件的D点共有3个，
以A、B、C、D四个点为顶点的四边形为平行四边形分别是
．
其中第四个顶点的坐标为：
D1（3，-4）或D2（7，-4）或D3（-1，0）
练习册系列答案
科学实验活动册系列答案
相关题目
