题目内容
做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A、B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获利润分别为30元和35元,乙店铺获利润分别为26元和36元.某日,王老板进A款式服装36件,B款式服装24件,并将这批服装分配给两个店铺各30件.
(1)怎样将这60件服装分配给两个店铺,能使两个店铺在销售完这批服装后所获利润相同?
(2)怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下,王老板获利的总利润最大?最大的总利润是多少?
(1)怎样将这60件服装分配给两个店铺,能使两个店铺在销售完这批服装后所获利润相同?
(2)怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下,王老板获利的总利润最大?最大的总利润是多少?
(1)分配到甲店的A款22件,B款8件;分配到乙店的A款14件,B款16件。(2)20件,1870元
试题分析:(1)解:设A款式服装分配到甲店铺为x件,则分配到乙店铺为(36-x)件;
B款式分配到甲店铺为(30-x)件,分配到乙店铺为(x-6)件.
根据题意得:30x+35×(30-x)=26×(36-x)+36(x-6)
解得x=22.
所以36-x=14(件),30-x=8(件),x-6=16(件)
(2)设总利润为w元,根据题意得
30x+35×(30-x)≥950,解得x≤20.
∴6≤x≤20.
w=30x+35×(30-x)+26×(36-x)+36(x-6)
=5x+1770 (6分)
∵k=5>0,∴w随x的增大而增大,
∴当x=20时,w有最大值1870.
本题涉及了一元一次方程、不等式组和一次函数与实际问题,该题是常考题,分析时较为复杂,要求学生读懂题意,列出提纲,再根据量与量之间的关系列出关系式,由关系式分析最佳方案。
B款式分配到甲店铺为(30-x)件,分配到乙店铺为(x-6)件.
根据题意得:30x+35×(30-x)=26×(36-x)+36(x-6)
解得x=22.
所以36-x=14(件),30-x=8(件),x-6=16(件)
(2)设总利润为w元,根据题意得
30x+35×(30-x)≥950,解得x≤20.
∴6≤x≤20.
w=30x+35×(30-x)+26×(36-x)+36(x-6)
=5x+1770 (6分)
∵k=5>0,∴w随x的增大而增大,
∴当x=20时,w有最大值1870.
本题涉及了一元一次方程、不等式组和一次函数与实际问题,该题是常考题,分析时较为复杂,要求学生读懂题意,列出提纲,再根据量与量之间的关系列出关系式,由关系式分析最佳方案。

练习册系列答案
相关题目
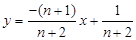 (n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2014= .
(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2014= . x+b,求n的值.
x+b,求n的值. 与一次函数
与一次函数 的图象交于A(3,1)、B(m,-3)两点.
的图象交于A(3,1)、B(m,-3)两点.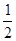 OA,请直接写出点P的坐标.
OA,请直接写出点P的坐标.
 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象. 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离
 与y=bx+c在同一直角坐标系内的大致图象是()
与y=bx+c在同一直角坐标系内的大致图象是()
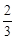 x+b与反比例函数y=
x+b与反比例函数y= 中,x与y的对应值如下表:
中,x与y的对应值如下表: