题目内容
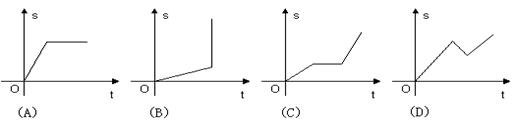
已知:甲、乙两车分别从相距300千米的 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)求甲车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.

 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.(1)求甲车离出发地的距离
 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;(2)当它们行驶到与各自出发地的距离相等时,用了
 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.

(1)当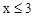 时, 函数为:
时, 函数为: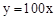 ;当
;当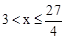 时, 函数为:
时, 函数为: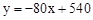 ;当
;当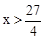 ,y=0.
,y=0.
(2) 乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式为:y=40x.
(小时)之间的函数关系式为:y=40x.
(3) 它们在行驶的过程中相遇的时间为: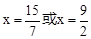 .
.
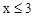 时, 函数为:
时, 函数为: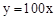 ;当
;当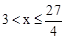 时, 函数为:
时, 函数为: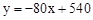 ;当
;当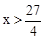 ,y=0.
,y=0.(2) 乙车离出发地的距离
 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式为:y=40x.
(小时)之间的函数关系式为:y=40x.(3) 它们在行驶的过程中相遇的时间为:
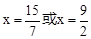 .
.根据分段函数图像写出分段函数.
试题分析:(1)当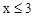 时甲的函数图像过点(0,0)和(3,300),此时函数为:
时甲的函数图像过点(0,0)和(3,300),此时函数为: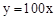 ,当x=3时甲到达B地,当
,当x=3时甲到达B地,当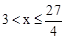 时过点(3,300)和点
时过点(3,300)和点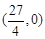 ,设此时函数为
,设此时函数为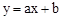 ,则可得到方程组:
,则可得到方程组: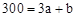 ,
,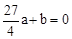 ,解得
,解得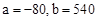 ∴
∴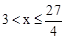 时函数为:
时函数为: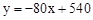 ,当
,当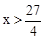 ,y=0.
,y=0.
(2)由图知乙的函数图像过点(0,0),设它的函数图像为:y="mx," ∵当它们行驶到与各自出发地的距离相等时,用了 小时,∴
小时,∴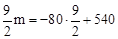 ,解得:m=40,∴乙车离出发地的距离
,解得:m=40,∴乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式为:y=40x.
(小时)之间的函数关系式为:y=40x.
(3)当它们在行驶的过程中,甲乙相遇两次即甲从A向B行驶的过程中相遇一次(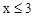 )和甲从B返回A的过程中相遇一次(
)和甲从B返回A的过程中相遇一次(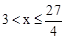 ),∴当
),∴当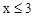 时,有
时,有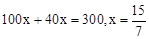 ;当
;当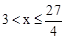 ,有
,有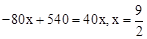 ,∴它们在行驶的过程中相遇的时间为:
,∴它们在行驶的过程中相遇的时间为: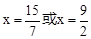 .
.
试题分析:(1)当
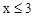 时甲的函数图像过点(0,0)和(3,300),此时函数为:
时甲的函数图像过点(0,0)和(3,300),此时函数为: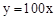 ,当x=3时甲到达B地,当
,当x=3时甲到达B地,当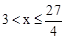 时过点(3,300)和点
时过点(3,300)和点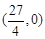 ,设此时函数为
,设此时函数为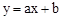 ,则可得到方程组:
,则可得到方程组: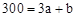 ,
,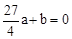 ,解得
,解得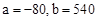 ∴
∴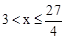 时函数为:
时函数为: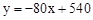 ,当
,当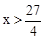 ,y=0.
,y=0.(2)由图知乙的函数图像过点(0,0),设它的函数图像为:y="mx," ∵当它们行驶到与各自出发地的距离相等时,用了
 小时,∴
小时,∴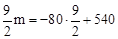 ,解得:m=40,∴乙车离出发地的距离
,解得:m=40,∴乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式为:y=40x.
(小时)之间的函数关系式为:y=40x.(3)当它们在行驶的过程中,甲乙相遇两次即甲从A向B行驶的过程中相遇一次(
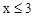 )和甲从B返回A的过程中相遇一次(
)和甲从B返回A的过程中相遇一次(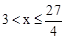 ),∴当
),∴当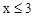 时,有
时,有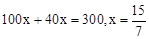 ;当
;当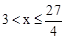 ,有
,有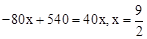 ,∴它们在行驶的过程中相遇的时间为:
,∴它们在行驶的过程中相遇的时间为: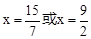 .
.
练习册系列答案
相关题目
 的两根.
的两根.
 中,一次函数
中,一次函数 和反比例函数
和反比例函数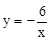 的图象都经过点
的图象都经过点 .
. 的值和一次函数的表达式;
的值和一次函数的表达式;
 x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.