题目内容
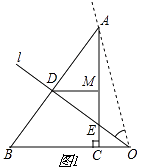
【题目】已知，如图，Rt△ABC，∠ACB=90°，BC=6，AC=8，O为BC延长线上一点，CO=3，过O，A作直线l，将l绕点O逆时针旋转，l与AB交于点D，与AC交于点E，当l与OB重合时，停止旋转；过D作DM⊥AE于M，设AD=x，S△ADE=S．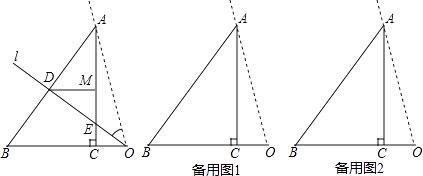
（1）用含x的代数式表示DM，AM的长；
（2）当直线l过AC中点时，求x的值；
（3）用含x的代数式表示AE的长；
（4）求S与x之间的函数关系式；
（5）当x为多少时，DO⊥AB．
【答案】
（1）
解：如图1，
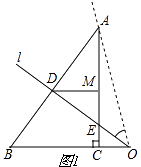
在Rt△ABC中，BC=6，AC=8，
∴AB=10，
∵DM⊥AC，BC⊥AC，
∴DM∥BC，
∴ 
，
∴ 
，
∴DM= 
x，
（2）
如图2，
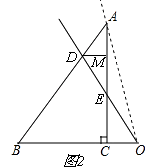
∵直线l过AC中点，
∴AE=CE= 
AC=4，
∵DM∥BC，
∴ 
，
∴ 
①，
∵DM∥BC，
∴ 
∴ 
，
∴ 
②，
由①②得，AM=ME= AE=2，
∵DM∥BC，
∴ 
，
∴ 
，
∴x= 
，
（3）
由（1）有，DM= x，
在Rt△ADM中，AM= 
x，
∴MC=8﹣AM=8﹣ x，
∵DM∥BC，
∴ 
，
∴ 
，
∴ 
，
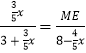∴ME= 
，
∴AE=AM+ME= 
，
（4）
解：由DM= x，AE= 
x﹣ 
x2，
∴S= AE×DM= × x×（ x﹣ x2）= 
x2﹣ 
x3，
（5）
解：∵DO⊥AB，
∴∠B+∠BOD=90°，
∵∠B+∠BAC=90°，
∴∠BOD=∠BAC，
∴△OBD∽△ABC，
∴ 
，
∴ 
，
∴BD=5.4，
∴x=AD=AB﹣BD=10﹣5.4=4.6．
【解析】探究1，根据勾股定理求出AB=10，再由DM∥BC，得出 ，求出DM；探究2，由直线l过AC中点，得到AE=CE= AC=4，再由DM∥BC， ， ，求出AM=ME= AE=2，从而求出x；探究3，由DM，AM，求出MC，再由DM∥BC，得出比例式求出ME，从而得到AE；发现：由探究1，得到DM，再由探究3，得到AE求出S；探究4，由DO⊥AB，得到∠B+∠BOD=90°，判断出△OBD∽△ABC，求出BD即可，
【考点精析】本题主要考查了平行线分线段成比例和相似三角形的应用的相关知识点，需要掌握三条平行线截两条直线，所得的对应线段成比例；测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解才能正确解答此题．
