题目内容
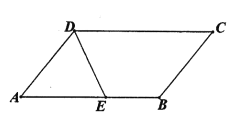
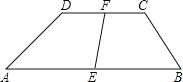
【题目】如图所示![]() 梯形ABCD中,
梯形ABCD中,![]() 分别为
分别为![]() 的中点,求EF.
的中点,求EF.
【答案】![]()
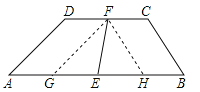
【解析】试题分析:过点F分别作FG∥AD,FH∥BC交AB于G,H,根据平行线的性质及三角形内角和定理可得△FGH是直角三角形,由平行四边形的判定定理可知四边形ADGF、FHBC都是平行四边形,利用线段之间的相等关系求出GH的长,再根据直角三角形的性质可求出EF的长.
试题解析:解:过点F分别作FG∥AD,FH∥BC交AB于G,H,如图,∴∠A=∠FGH,∠B=∠FHG.∵∠B+∠A=90°,∴∠FGH+∠FHG=90°,∴△FGH是直角三角形.∵FG∥AD,FH∥BC,AB∥CD,∴四边形ADFG、FHBC都是平行四边形.又∵E、F分别是两底的中点,∴AE=EB,BH=AG,∴GE=EH,∴DF=AG=![]() ,FC=HB=
,FC=HB=![]() ,FG=AD,FH=BC,在Rt△FGH中,即EF是Rt△FGH斜边的中线,∴EF=
,FG=AD,FH=BC,在Rt△FGH中,即EF是Rt△FGH斜边的中线,∴EF=![]() GH=
GH=![]() (AB﹣CD)=
(AB﹣CD)=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目