题目内容
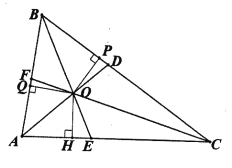
【题目】如图，∠ADC=130°，∠ABC=∠ADC，BF、DE分别平分∠ABC与∠ADC，交对边于F、E，且∠ABF=∠AED，过E作EH⊥AD交AD于H。
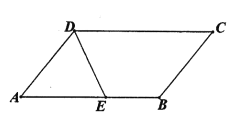
（1）在图中作出线段BF和EH（不要求尺规作图）；
（2）求∠AEH的大小。
小亮同学根据条件进行推理计算，得出结论，请你在括号内注明理由。
证明：∵BF、DE分别平分∠ABC与∠ADC，（已知）
∴∠ABF=
∠ABC，∠CDE=∠ADC。（ ）
∵∠ABC=∠ADC，（已知）
∴∠ABF=∠CDE。（等式的性质）
∵∠ABF=∠AED，（已知）
∴∠CDE=∠AED。（ ）
∴AB∥CD。（ ）
∵∠ADC=130°（已知）
∴∠A=180°-∠ADC=50°（两直线平行，同旁内角互补）
∵EH⊥AD于H（已知）
∴∠EHA=90°（垂直的定义）
∴在Rt△AEH中，∠AEH=90°-∠A（ ）=40°。
【答案】（1）见解析；（2）见解析
【解析】
（1）根据题意作图即可；
（2）根据证明过程写出相应的理由即可.
作∠ABC的平分线BF, 过E作EH⊥AD交AD于H,如图所示
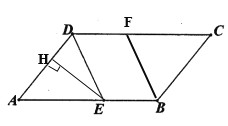
（2） 角平分线性质 等式的性质 内错角相等，两直线平行 在直角三角形中，两锐角互余
练习册系列答案
相关题目
