Question

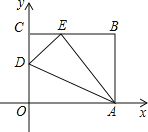
【题目】如图，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，则D点的坐标是 ．

Answer 1

【答案】（0，5）

【解析】

试题分析：先由矩形的性质得到AB=OC=8，BC=OA=10，再根据折叠的性质得AE=AO=10，DE=DO，在Rt△ABE中，利用勾股定理可计算出BE=6，则CE=BC﹣BE=4，设OD=x，则DE=x，DC=8﹣x，在Rt△CDE中根据勾股定理有x2=（8﹣x）2+42，解方程求出x，即可确定D点坐标．

解：∵四边形ABCD为矩形，

∴AB=OC=8，BC=OA=10，

∵纸片沿AD翻折，使点O落在BC边上的点E处，

∴AE=AO=10，DE=DO，

在Rt△ABE中，AB=8，AE=10，

∴BE==6，

∴CE=BC﹣BE=4，

设OD=x，则DE=x，DC=8﹣x，

在Rt△CDE中，∵DE2=CD2+CE2，

∴x2=（8﹣x）2+42，

∴x=5，

∴D点坐标为（0，5）．

故答案为（0，5）．