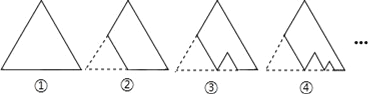
��Ŀ����
����Ŀ������ABC�У�BC=AC����C=90����ֱ�Ƕ���C��x���ϣ�һ��Ƕ���B��y���ϣ�
��1����ͼ����AD�ڴ�ֱx�ᣬ����Ϊ��D����C�����ǣ���1��0������A�������ǣ���3��1�������B�����꣮
��2����ͼ����ֱ�DZ�BC�����������ϻ�������y��ǡ��ƽ����ABC��AC��y�ύ�ڵ�D������A��AE��y����E�������BD��AE��������������ϵ����֤����IJ��룮
��3����ͼ����ֱ�DZ�BC�����������ϻ�����ʹ��A�ڵ��������ڣ���A����AF��y����F���ڻ����Ĺ����У������OC��AF��OB֮���������Ĺ�ϵ��ֱ��д�����ۣ�����Ҫ֤����

���𰸡���1����0��2������2��BD=2AF����3��OC=OB+AF.
�������������������1��ֻҪ���Rt��ADC��Rt��COB������
��2����˵��BD��AE��������������ϵ��Ȼ����Եõ���������ϵ���������ʵĸ����ߣ�������Ӧ��ͼ�Σ����ݵ��������εױ��ϵĸߡ��ױ��ϵ����ߡ����ǵ�ƽ�������ߺ�һ����������֤����Ҫ˵����������ϵ��
��3���Ȳ���OC��AF��OB֮��Ĺ�ϵ��Ȼ����ݲ����������ʵĸ����ߣ�������Ӧ��ͼ�Σ�Ȼ��֤����Ҫ֤���Ľ��ۼ��ɣ�
���������(1)�ߵ�C������(1,0),��A��������(3,1)
��AD=OC��
��Rt��ADC��Rt��COB���� ![]() ��
��
��Rt��ADC��Rt��COB(HL)��
��OB=CD=2��
���B��������(0��2)��
(2)BD=2AF��
���ɣ���AE���ӳ��߽�BC���ӳ����ڵ�F������ͼ��ʾ��
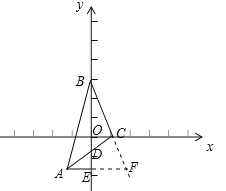
����ABC�ǵ���ֱ�������Σ�BC=AC��ֱ�Ƕ���C��x���ϣ�AE��y����E��
���BCA=��ACF=90������AED=90����
���DBC+��BDC=90������DAE+��ADE=90����
�ߡ�BDC=��ADE��
���DBC=��FAC��
����BDC����AFC��
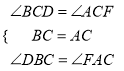 ��
��
����BDC����AFC(ASA)
��BD=AF��
��BE��AE��y��ǡ��ƽ�֡�ABC��
��AF=2AE��
��BD=2AF��
(3)OC=OB+AF��
֤������AE��OC�ڵ�E������ͼ��ʾ��

��AE��OC��AF��y�ᣬ
���ı���OFAE�Ǿ�������AEC=90����
��AF=OE��
����ABC�ǵ���ֱ����������BC=AC��ֱ�Ƕ���C��x��������BOC=90����
���BCA=90����
���BCO+��CBO=90������BCO+��ACE=90����
���CBO=��ACE��
����BOC����CEO��
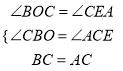 ��
��
����BOC����CEO(AAS)
��OB=CE��
��OC=OE+EC��OE=AF��OB=EC��
��OC=OB+AF.

 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�