Question

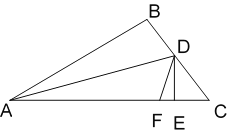
【题目】已知，如图，在△ABC中，AD平分∠BAC，DE、DF分别是△ADC的高和角平分线（∠C >∠DAC）.

（1）若∠B=80°，∠C=40°，求∠DAE的度数；

（2）试猜想∠EDF、∠C与∠DAC有何种关系？并说明理由.

Answer 1

【答案】（1）；（2） ，理由见解析.

【解析】试题分析:(1)先利用三角形内角和定理计算出∠,然后利用角平分线的定义可得∠DAE= ,(2)根据三角形内角和定理可得: ∠-∠DAC-∠C,利用角平分线的定义可得: ∠CDF=∠= (-∠DAC-∠C)=90°－ (∠DAC+∠C),利用直角三角形两锐角互余可得: ∠CDE=90°－∠C,所以∠EDF=∠CDF－∠CDE= (∠C－∠DAC).试题解析:（1）在 中， ,,

,

平分,

,

(2) 理由如下:

在中,

, ,

平分,,

是的高, ,

.