题目内容
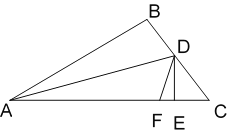
【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求证:∠AGD=90°
(2)求图1中重叠部分(△DCG)的面积;
(3)合作交流:“希望”小组受问题(1)(2)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.

【答案】(1)证明见解析;(2)6;(3)![]() .
.
【解析】试题分析:(1)由D点是AB的中点易得AD=BD=CD,所以∠DCB=∠DBC;再由△ABC≌△FDE得∠FDE=∠B,从而∠FDE=∠DCB,所以DG∥BC,进而可证∠DGC=90°;
(2)由(1)得DG⊥AC,G是AC的中点.即可求出S△DCG=![]() ×CGDG=
×CGDG=![]() ×4×3=6;
×4×3=6;
(2)如图2所示:先证明AG=GH,再求出AD=![]() AB=5,然后证明△ADH∽△ACB,得出比例式
AB=5,然后证明△ADH∽△ACB,得出比例式![]() ,求出DH=
,求出DH=![]() ,即可求出S△DGH=
,即可求出S△DGH=![]() S△ADH=
S△ADH=![]() ×
×![]() ×DHAD=
×DHAD=![]() ×
×![]() ×5=
×5=![]()
试题解析:(1)∵∠ACB=90°,D是AB的中点,
∴DC=DB=DA.
∴∠B=∠DCB.
又∵△ABC≌△FDE,
∴∠FDE=∠B.
∴∠FDE=∠DCB.
∴DG∥BC.
∴∠AGD=∠ACB=90°.
∴DG⊥AC.
∴∠DGC=90°;
(2)由(1)知:DG⊥AC
∵DC=DA,
∴G是AC的中点.
∴CG=![]() AC=
AC=![]() ×8=4,DG=
×8=4,DG=![]() BC=
BC=![]() ×6=3.
×6=3.
∴S△DCG=![]() ×CGDG=
×CGDG=![]() ×4×3=6.
×4×3=6.
(3)如图2所示:
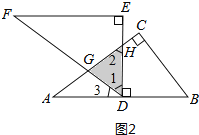
∵△ABC≌△FDE,
∴∠B=∠1.
∵∠C=90°,ED⊥AB,
∴∠A+∠B=90°,∠A+∠2=90°,
∴∠B=∠2,
∴∠1=∠2,
∴GH=GD,
∵∠A+∠2=90°,∠1+∠3=90°,
∴∠A=∠3,
∴AG=GD,
∴AG=GH,
∴点G为AH的中点;
在Rt△ABC中,AB=![]() =10,
=10,
∵D是AB中点,
∴AD=![]() AB=5,
AB=5,
在△ADH与△ACB中,∵∠A=∠A,∠ADH=∠ACB=90°,
∴△ADH∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() .
.
∴S△DGH=![]() S△ADH=
S△ADH=![]() ×
×![]() ×DHAD=
×DHAD=![]() ×
×![]() ×5=
×5=![]() .
.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案