Question

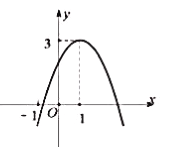
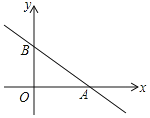
【题目】如图，直线与坐标轴相交于A、B两点，点P为x轴正半轴上的一个动点，当△PAB是等腰三角形时，点P的坐标为_____．

Answer 1

【答案】（，0）或（9，0）．

【解析】

利用一次函数图象上点的坐标特征可求出点A，B的坐标，利用勾股定理可求出AB的长，分PA＝PB和AB＝AP两种情况考虑：①当PA＝PB时，设点P的坐标为（m，0），利用PA＝PB可得出关于m的方程，解之即可得出点P的坐标；②当AB＝AP时，由AB＝5可得出AP＝5，结合OA＝4可得出OP的长，进而可得出点P的坐标．综上，此题得解．

解：当x＝0时，y＝﹣x+3＝3，

∴OB＝3，点B的坐标为（0，3）；

当y＝0时，﹣x+3＝0，解得：x＝4，

∴OA＝4，点A的坐标为（4，0）．

∴AB＝＝5

分两种情况考虑，如图所示．

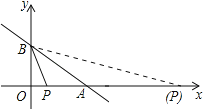
①当PA＝PB时，设点P的坐标为（m，0），则PA＝4﹣m，PB＝，

∴4﹣m＝，

解得：m＝，

∴点P的坐标为（，0）；

②当AB＝AP时，AP＝5，

∴OP＝OA+AP＝9，

∴点P的坐标为（9，0）．

故答案为：（，0）或（9，0）．