题目内容
下列结论正确的是
- A.所有直角三角形都相似
- B.所有边长相等的菱形都相似
- C.同弧所对的圆周角相等
- D.当b2-4ac=0时，二次函数y=ax2+bx+c的图象与坐标轴只有一个交点
C
分析：根据相似三角形的判定和性质，圆周角定理，二次函数以及相似多边形的性质，采用排除法，逐项分析判断．
解答：A、所有直角三角形都相似，错误，因为它们的锐角不一定相等；
B、所有边长相等的菱形都相似，错误，因为它们的角不一定相等；
C、同弧所对的圆周角相等，正确；
D、当b2-4ac=0时，二次函数y=ax2+bx+c的图象与坐标轴只有一个交点，错误，因为图象与x轴只有一个交点，与y轴还有一个交点．
故选C．
点评：本题主要考查了相似三角形的判定和性质，圆周角定理，二次函数以及相似多边形的性质等知识点．
分析：根据相似三角形的判定和性质，圆周角定理，二次函数以及相似多边形的性质，采用排除法，逐项分析判断．
解答：A、所有直角三角形都相似，错误，因为它们的锐角不一定相等；
B、所有边长相等的菱形都相似，错误，因为它们的角不一定相等；
C、同弧所对的圆周角相等，正确；
D、当b2-4ac=0时，二次函数y=ax2+bx+c的图象与坐标轴只有一个交点，错误，因为图象与x轴只有一个交点，与y轴还有一个交点．
故选C．
点评：本题主要考查了相似三角形的判定和性质，圆周角定理，二次函数以及相似多边形的性质等知识点．
练习册系列答案
名校课堂系列答案
相关题目
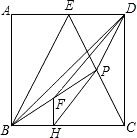如图，已知边长为4的正方形ABCD中，E为AD中点，P为CE中点，F为BP中点，FH⊥BC交BC于H，连接PH，则下列结论正确的是（ ）①BE=CE；②sin∠EBP=
| 1 |
| 2 |
| A、①④⑤ | B、①②③ |
| C、①②④ | D、①③④ |
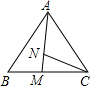如图，点M在BC上，点N在AM上，CM=CN，| AM |
| AN |
| BM |
| CM |
| A、△ABM∽△ACB |
| B、△ANC∽△AMB |
| C、△ANC∽△ACM |
| D、△CMN∽△BCA |
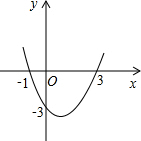已知二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（ ）
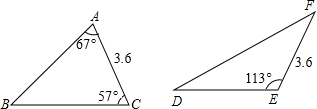如图，△ABC中BC边上的高为h1，AB边上的高为h2，△DEF中DE边上的高为h3，下列结论正确的是（ ）