题目内容
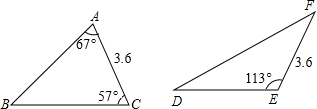 如图,△ABC中BC边上的高为h1,AB边上的高为h2,△DEF中DE边上的高为h3,下列结论正确的是( )
如图,△ABC中BC边上的高为h1,AB边上的高为h2,△DEF中DE边上的高为h3,下列结论正确的是( )分析:过A作AN⊥BC于N,过C作CM⊥AB于M,过F作FQ⊥DE,交DE延长线于Q,求出AC=EF,∠Q=∠AMC,∠BAC=∠FEQ,根据AAS推出△AMC≌△EQF即可.
解答:解:
过A作AN⊥BC于N,过C作CM⊥AB于M,过F作FQ⊥DE,交DE延长线于Q,
则∠Q=∠CMA=90°,
∵AC=3.6,EF=3.6,
∴AC=EF,
∵∠FED=113°,
∴∠FEQ=180°-113°=67°=∠BAC,
在△AMC和△EQF中
∴△AMC≌△EQF,
∴CM=FQ,
即h2=h3,
不能推出h1和h2的关系,也不能求出h1和h3的关系,
故选B.

过A作AN⊥BC于N,过C作CM⊥AB于M,过F作FQ⊥DE,交DE延长线于Q,
则∠Q=∠CMA=90°,
∵AC=3.6,EF=3.6,
∴AC=EF,
∵∠FED=113°,
∴∠FEQ=180°-113°=67°=∠BAC,
在△AMC和△EQF中
|
∴△AMC≌△EQF,
∴CM=FQ,
即h2=h3,
不能推出h1和h2的关系,也不能求出h1和h3的关系,
故选B.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应边相等.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

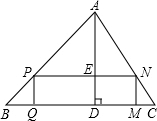 已知如图,△ABC中BC=60cm,高AD=40cm,四边形PQMN是矩形,点P在AB边上,点Q、M在BC边上,点N在AC边上.
已知如图,△ABC中BC=60cm,高AD=40cm,四边形PQMN是矩形,点P在AB边上,点Q、M在BC边上,点N在AC边上. 如图,△ABC中BC边上的高是( )
如图,△ABC中BC边上的高是( ) 如图,△ABC中BC边上的高为
如图,△ABC中BC边上的高为