题目内容
【题目】如图，在ABCD中，AE=CG，BF=DH，连接EF，FG，GH，HE．求证：四边形EFGH是平行四边形． 
【答案】证明：∵四边形ABCD是平行四边形，
∴∠A=∠C，∠B=∠D，AD=BC，
又∵BF=DH，
∴CF=AH，
在△AEH和△CGF中，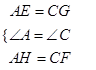 
，
∴△AEH≌△CGF（SAS），
∴EH=GF；同理：GH=EF；
∴四边形EFGH是平行四边形
【解析】易证得△AEH≌△CGF，从而证得EH=GF，同理GH=EF，根据两组对边分别相等的四边形是平行四边形得证．
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识，掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
