题目内容
已知y=ax2+bx+c经过点（2，1）、（-1，-8）、（0，-3）．
（1）求这个抛物线的解析式；
（2）画出该抛物线的草图、并标出图象与x轴交点的横坐标；
（3）观察你所画的抛物线的草图，写出x在什么范围内取值时，函数值y＜0？
解：（1）把点（2，1），（-1，-8），（0，-3）代入可得
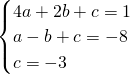
解得a=-1，b=4，c=-3
故y=-x2+4x-3；
（2）当y=0时，-x2+4x-3=0
解得x=1或x=3
故图象与x轴交点的横坐标是1和3；
（3）当x＜1或x＞3时，函数值y＜0．
分析：（1）直接利用图中的三个点的坐标代入解析式用待定系数法求解析式；
（2）令y=0，解关于x的一元二次方程-x2+4x-3=0，其解即为图象与x轴交点的横坐标；
（3）依据图象可知，当图象在x轴上方时，y＞0，在x轴下方时，y＜0，在x轴上时，y=0．
点评：主要考查了用待定系数法求二次函数的解析式和二次函数及其图象的性质．
练习册系列答案
相关题目
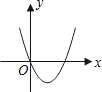已知y=ax2+bx+c的图象如图所示，则y=ax+b的图象一定过（ ）| A、第一，二，三象限 | B、第一，二，四象限 | C、第二，三，四象限 | D、第一，三，四象限 |
已知y=ax2+bx+c的图象如图，那么关于x的方程ax2+bx+c-3=0的根的情况（ ）