题目内容
【题目】已知,如图1,在 ![]() 中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
(1)求证: ![]() 是等腰三角形。
是等腰三角形。
(2)如图2,若将上图中的两个全等的矩形改为两个全等的正三角形( ![]() 和
和 ![]() ),其他条件不变。请探究
),其他条件不变。请探究 ![]() 的形状,并说明理由。
的形状,并说明理由。
(3)若将上图中的两个全等的矩形改为两个正方形,并把 ![]() 中的边BC缩短到如图3形状,请探究
中的边BC缩短到如图3形状,请探究 ![]() 的形状,并说明理由。
的形状,并说明理由。
【答案】
(1)
证明:∵四边形CEGH和CFMN是全等的矩形,
∴CE=CF,EG=FM,∠GEC=∠MFC= 90°.
连接DE、DF,如图1.

∵D、E、F分别是AB、AC、BC的中点,
∴DE∥BC,且DE=CF=![]() BC;
BC;
DF∥AC,且DF=CE=![]() AC.
AC.
∴四边形DECF是平行四边形.
∴ ∠DEC=∠DFC.
又∵∠GEC=∠MFC,∴∠DEG=∠DFM.
∵AC=BC,∴DE=DF.
∴△DEG ≌ △DFM(SAS).
∴DG=DM.
∴△DGM是等腰三角形.
(2)
解:△DGM是等边三角形.
证明:∵△CEG和△CFM是全等的等边三角形,
∴CE =EG =CG=CF=FM=CM,∠GEC =∠MFC = 60°.
连接DE、DF,如图2.
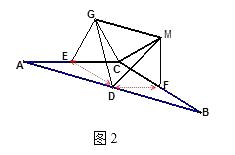
∵D、E、F分别是AB、AC、BC的中点,
∴DE∥BC,且DE = CF
=![]() BC,DF∥AC,且DF = CE =
BC,DF∥AC,且DF = CE =![]() AC.
AC.
∴四边形DECF是平行四边形.
∴ ∠DEC =∠DFC.
又∵∠GEC =∠MFC,∴∠DEG=∠DFM.
∵AC=BC,∴DE=DF.
∴△DEG ≌ △DFM(SAS).
∴DG=DM.
∴△DGM是等腰三角形.
又∵∠GCM+∠ACB=360°-60°-60°=240°
∠GED+∠ACB=∠GEC+∠CED+∠ACB=60°+180°=240°
∴∠GCM=∠GED
又DE=CF=CM,EG=CG
∴△GED≌ △GCM(SAS).
∴GM=GD
∴△DGM是等边三角形.
(3)
解:△DGM是等腰直角三角形.

显然,由(1)(2)易得△DEG≌ △MFD(SAS)
∴DG=DM,∠DGE=∠MDF
∵DF∥AC
∴∠CED+∠EDF=180°
即:∠CED+∠EDG+∠GDM+∠MDF=180°
又由三角形内角和可知∠CED+∠EDG+∠GEC+∠DGE=180°
∴∠GDM=∠GEC=90°
∴△DGM是等腰直角三角形.
【解析】三个小题都要证明△DFM≌ △DFM(SAS),证明方法类似;再根据全等的性质和每小题的不同点证明得到答案.
【考点精析】本题主要考查了三角形中位线定理和矩形的性质的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案



