题目内容
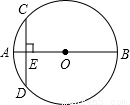
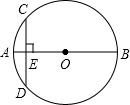
如图,AB为⊙O的直径,CD与⊙O相切于点C,且OD⊥BC,垂足为F,OD交⊙O于点E.
![]()
![]()
1)证明:BE=CE
(2)证明:∠D=∠AEC;
(3)若⊙O的半径为5,BC=8,求△CDE的面积.
 |
解:(1)∵BC是⊙O的弦,半径OE⊥BC
![]()
![]()
∴BE=CE
(2)连结OC
∵CD与⊙O相切于点C
∴∠OCD=90°
∴∠OCB+∠DCF=90°
∵∠D+∠DCF=90°
∴∠OCB=∠D
∵OB=OC
∴∠OCB=∠B
∵∠B=∠AEC
∴∠D=∠AEC
 |
(3)在Rt△OCF中,OC=5,CF=4
∴![]()
∵∠COF=∠DOC,∠OFC=∠OCD
∴Rt△OCF∽Rt△ODC
∴![]() ,即
,即![]() …………9分
…………9分
∴![]()
∴![]()
注:本小题也可利用Rt△OCD∽Rt△ACB等,以及S△CDE=S△OCD-S△OCE求解.

练习册系列答案
相关题目
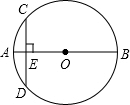 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
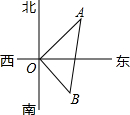 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为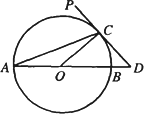
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为