题目内容
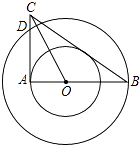
【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE. 
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
【答案】
(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠DEC,
∴∠A=∠AEB
(2)证明:∵DC⊥OE,
∴DF=CF,
∴OE是CD的垂直平分线,
∴ED=EC,又DE=DC,
∴△DEC为等边三角形,
∴∠AEB=60°,又∠A=∠AEB,
∴△ABE是等边三角形.
【解析】(1)根据圆内接四边形的性质得到∠A=∠DCE,根据等腰三角形的性质得到∠DCE=∠DEC,等量代换证明结论;(2)根据垂径定理得到OE是CD的垂直平分线,根据题意证明△DEC为等边三角形,证明结论.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆内接四边形的性质的理解,了解把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目