题目内容
【题目】四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1 , S2 , 则|S1﹣S2|=(平方单位) 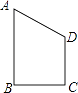
【答案】4π
【解析】解:绕AB旋转一周形成的圆柱的侧面的面积是:2π×2×2=8π; 绕CD旋转一周形成的圆柱的侧面的面积是:2π×2×3=12π,
则|S1﹣S2|=4π.
故答案是:4π.
【考点精析】认真审题,首先需要了解点、线、面、体的认识(点:线和线相交的地方是点,它是几何图形中最基本的图形;线:面和面相交的地方是线,分为直线和曲线;面:包围着体的是面,分为平面和曲面;体:几何体也简称体),还要掌握圆锥的相关计算(圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h.)的相关知识才是答题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目