题目内容
【题目】直线ax+by+c=0与圆O:x2+y2=16相交于两点M、N,若c2=a2+b2 , P为圆O上任意一点,则 ![]() 的取值范围是 .
的取值范围是 .
【答案】[﹣6.10]
【解析】解:取MN的中点A,连接OA,则OA⊥MN, ∵c2=a2+b2 ,
∴O点到直线MN的距离OA= ![]() =1,
=1,
x2+y2=16的半径r=4,
∴Rt△AON中,设∠AON=θ,得cosθ= ![]() =
= ![]() ,
,
cos∠MON=cos2θ=2cos2θ﹣1= ![]() ﹣1=﹣
﹣1=﹣ ![]() ,
,
由此可得, ![]()
![]() =|
=| ![]() ||
|| ![]() |cos∠MON
|cos∠MON
=4×4×(﹣ ![]() )=﹣14,
)=﹣14,
则 ![]() =(
=( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=
)= ![]()
![]() +
+ ![]() 2﹣
2﹣ ![]() (
( ![]() +
+ ![]() )
)
=﹣14+16﹣2 ![]()
![]() =2﹣2|
=2﹣2| ![]() ||
|| ![]() |cos∠AOP=2﹣8cos∠AOP,
|cos∠AOP=2﹣8cos∠AOP,
当 ![]() ,
, ![]() 同向时,取得最小值且为2﹣8=﹣6,
同向时,取得最小值且为2﹣8=﹣6,
当 ![]() ,
, ![]() 反向时,取得最大值且为2+8=10.
反向时,取得最大值且为2+8=10.
则 ![]() 的取值范围是[﹣6.10].
的取值范围是[﹣6.10].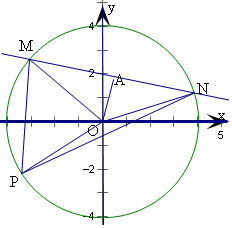
所以答案是:[﹣6.10].

练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M、p及图中a的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率.
