题目内容
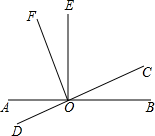
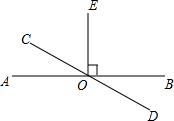
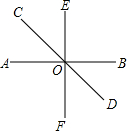
如图，直线AB，CD，EF相交于点O，OC平分∠AOE，且∠AOC：∠BOE=1：2．
（1）直线AB与EF互相垂直吗？判断并说明理由；
（2）求∠AOD的度数．
（1）直线AB与EF互相垂直吗？判断并说明理由；
（2）求∠AOD的度数．
（1）AB与EF互相垂直；
∵OC平分∠AOE，
∴∠AOC=∠COE，
设∠AOC=x°，则∠COE=x°，∠BOE=2x°，
x+x+2x=180，
解得：x=45，
∴∠EOB=90°，
∴EF⊥AB；
（2）∵∠EOB=90°，∠AOC=45°，
∴∠AOF=90°，∠DOF=45°，
∴∠AOD=135°．
∵OC平分∠AOE，
∴∠AOC=∠COE，
设∠AOC=x°，则∠COE=x°，∠BOE=2x°，
x+x+2x=180，
解得：x=45，
∴∠EOB=90°，
∴EF⊥AB；
（2）∵∠EOB=90°，∠AOC=45°，
∴∠AOF=90°，∠DOF=45°，
∴∠AOD=135°．
练习册系列答案
名校课堂系列答案
相关题目
