题目内容
求下列式子有意义的x的取值范围:(1)| (x+1)(2-x) |
| (x+1) |
| (2-x) |
| -|x| |
分析:根据二次根式的性质,被开方数大于或等于0,就可以求解.
解答:解:(1)由题意,得
,
解得-1≤x≤2,
当-1≤x≤2时,(x+1)(2-x)≥0.
故等式
=
•
成立时,x的取值范围是-1≤x≤2;
(2)由题意,得-|x|≥0,
∴|x|≤0,
又∵|x|≥0,
∴x=0.
故当x=0时,
有意义.
|
解得-1≤x≤2,
当-1≤x≤2时,(x+1)(2-x)≥0.
故等式
| (x+1)(2-x) |
| (x+1) |
| (2-x) |
(2)由题意,得-|x|≥0,
∴|x|≤0,
又∵|x|≥0,
∴x=0.
故当x=0时,
| -|x| |
点评:本题主要考查了二次根式、绝对值的性质及一元一次不等式组的解法.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
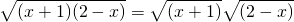 ; (2)
; (2)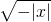 .
.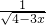 (2)
(2)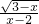 (3)
(3)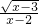 (4)
(4)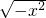 (5)
(5)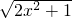 (6)
(6)