题目内容
求下列式子有意义的x的取值范围(1)
| 1 | ||
|
| ||
| x-2 |
| ||
| x-2 |
| -x2 |
| 2x2+1 |
| 2x-3 |
| 3-2x |
分析:(1)(2)(3)根据二次根式的性质和分式的意义,由被开方数大于等于0,分母不等于0可知;
(4)(5)(6)根据二次根式的意义,被开方数是非负数可知.
(4)(5)(6)根据二次根式的意义,被开方数是非负数可知.
解答:解:(1)根据二次根式的意义和分式有意义的条件,
被开方数4-3x≥0,分母4-3x≠0,
解得x<
.
所以x的取值范围是x<
.
(2)根据二次根式的意义和分式有意义的条件,
被开方数3-x≥0,解得x≤3;
分母x+2≠0,解得x≠-2.
所以x的取值范围是x≤3且x≠-2.
(3)根据二次根式的意义和分式有意义的条件,
被开方数x-3≥0,解得x≥3;
分母x-2≠0,解得x≠2.
因为大于或等于3的数中不包含2这个数,
所以x的取值范围是x≥3.
(4)根据题意得:-x2≥0,
∵x2≥0,
∴x2=0,
解得x=0.
∴x的取值范围是x=0;
(5)根据题意得:2x2+1≥0,
∵x2≥0,
∴2x2+1>0,
故x的取值范围是任意实数;
(6)根据题意得:2x-3≥0,解得x≥
;
2x-3≤0,解得x≤
.
综上,可知x=
.
∴x的取值范围是x=
.
被开方数4-3x≥0,分母4-3x≠0,
解得x<
| 4 |
| 3 |
所以x的取值范围是x<
| 4 |
| 3 |
(2)根据二次根式的意义和分式有意义的条件,
被开方数3-x≥0,解得x≤3;
分母x+2≠0,解得x≠-2.
所以x的取值范围是x≤3且x≠-2.
(3)根据二次根式的意义和分式有意义的条件,
被开方数x-3≥0,解得x≥3;
分母x-2≠0,解得x≠2.
因为大于或等于3的数中不包含2这个数,
所以x的取值范围是x≥3.
(4)根据题意得:-x2≥0,
∵x2≥0,
∴x2=0,
解得x=0.
∴x的取值范围是x=0;
(5)根据题意得:2x2+1≥0,
∵x2≥0,
∴2x2+1>0,
故x的取值范围是任意实数;
(6)根据题意得:2x-3≥0,解得x≥
| 3 |
| 2 |
2x-3≤0,解得x≤
| 3 |
| 2 |
综上,可知x=
| 3 |
| 2 |
∴x的取值范围是x=
| 3 |
| 2 |
点评:本题主要考查了二次根式的意义和性质.概念:式子
(a≥0)叫二次根式.
性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.
当二次根式在分母上时还要考虑分母不等于零,此时被开方数大于0.
| a |
性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.
当二次根式在分母上时还要考虑分母不等于零,此时被开方数大于0.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
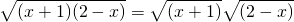 ; (2)
; (2)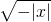 .
.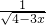 (2)
(2)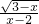 (3)
(3)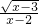 (4)
(4)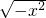 (5)
(5)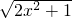 (6)
(6)