题目内容
设∠MON=20º,A为OM上一点OA=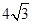 ,D为ON上一点,OD=
,D为ON上一点,OD=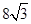 ,C为AM上任一点,B是OD上任一点,那么折线ABCD的长AB+BC+CD 最小值是( )
,C为AM上任一点,B是OD上任一点,那么折线ABCD的长AB+BC+CD 最小值是( )
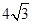 ,D为ON上一点,OD=
,D为ON上一点,OD=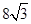 ,C为AM上任一点,B是OD上任一点,那么折线ABCD的长AB+BC+CD 最小值是( )
,C为AM上任一点,B是OD上任一点,那么折线ABCD的长AB+BC+CD 最小值是( ) | A.12 | B.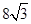 | C. 8 | D.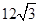 |
A
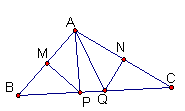
解:如图,分别作A、D关于ON、OM的对称点A′、D′点,连接A′B、CD′、A′D′,
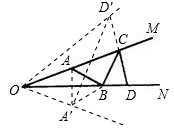
则A′B=AB,CD′=CD,
∴AB+AC+CD≥A′B+BC+CD′,
显然A′B+BC+CD′≥A′D′,
∵∠A′ON=∠NOM=MOD′=20°,∴∠D′OA′=60°,
又OA′=OA=4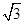 ,OD′=OD=8
,OD′=OD=8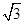 ,即
,即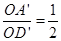
而cos60°= ,∴cos60°=
,∴cos60°=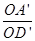
∴△D′OA′为直角三角形,且∠OA′D′=90°,
∴A′D′= =12
=12
故选A

则A′B=AB,CD′=CD,
∴AB+AC+CD≥A′B+BC+CD′,
显然A′B+BC+CD′≥A′D′,
∵∠A′ON=∠NOM=MOD′=20°,∴∠D′OA′=60°,
又OA′=OA=4
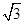 ,OD′=OD=8
,OD′=OD=8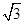 ,即
,即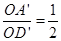
而cos60°=
 ,∴cos60°=
,∴cos60°=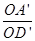
∴△D′OA′为直角三角形,且∠OA′D′=90°,
∴A′D′=
 =12
=12故选A

练习册系列答案
相关题目
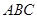 中,
中,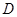 为
为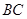 边的中点,过
边的中点,过 ∥
∥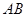 交
交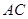 于点
于点 ,
,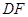 ∥
∥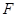 .
.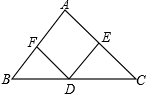
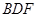 ≌△
≌△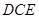 ;
; 中,
中, ,AC=3 ,BC=4,将它的一个锐角翻折,使该锐角顶点落在其对边的中点
,AC=3 ,BC=4,将它的一个锐角翻折,使该锐角顶点落在其对边的中点 处,折痕交另一直角边于
处,折痕交另一直角边于 ,交斜边于
,交斜边于 ,则
,则 的周长为
的周长为