��Ŀ����
����Ŀ����ͼ����ֱ������ϵ����һֱ��������AOB��OΪ����ԭ�㣬OA=1��tan��BAO=3��������������ԭ��O��ʱ����ת90�����õ���DOC��������y=ax2+bx+c������A��B��C��
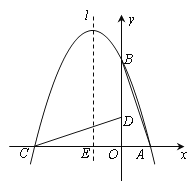
��1���������ߵĽ���ʽ��
��2������P�ǵڶ��������������ϵĶ��㣬�������Ϊt��
���������߶Գ���l��x�ύ��һ��E������PE����CD��F���������CEF����COD����ʱ��P�����꣮
![]() ���Ƿ����һ��P��ʹ��PCD�������������ڣ������PCD��������ֵ���������ڣ���˵�����ɣ�
���Ƿ����һ��P��ʹ��PCD�������������ڣ������PCD��������ֵ���������ڣ���˵�����ɣ�
���𰸡���1�� �����ߵĽ���ʽΪy=-x2-2x+3����2�� ����-1��4����-2��3������![]() ��
��
��������
�����������1�������A��B��C�����꣬�����ô���ϵ�����Ϳ���ֱ��������κ����Ľ���ʽ��
��2�����ɣ�1���Ľ���ʽ������������ߵĶԳ��ᣬ�������۵���CEF=90��ʱ������CFE=90��ʱ���������������ε����ʾͿ������P������ꣻ
�������ô���ϵ�������ֱ��CD�Ľ���ʽ����PM��CD�Ľ���ΪN������CD�Ľ���ʽ��ʾ����N�����꣬�ٸ���S��PCD=S��PCN+S��PDN�Ϳ��Ա�ʾ��������PCD����������ö���ʽ�Ϳ���������ۣ�
�����������1����Rt��AOB��OA=1��tan��BAO=![]() =3��
=3��
��OB=3OA=3��
�ߡ�DOC������AOB�Ƶ�O��ʱ����ת90�����õ��ģ�
���DOC�ա�AOB��
��OC=OB=3��OD=OA=1��
��A��B��C������ֱ�Ϊ��1��0������0��3����-3��0����
�������ʽΪ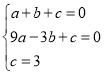 ����ã�
����ã�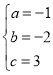 ��
��
�������ߵĽ���ʽΪy=-x2-2x+3��
��2���١������ߵĽ���ʽΪy=-x2-2x+3��
���Գ���l=-![]() =-1��
=-1��
��E���������-1��0����
��ͼ������CEF=90��ʱ����CEF�ס�COD����ʱ��P�ڶԳ����ϣ�����PΪ�����ߵĶ��㣬P��-1��4����
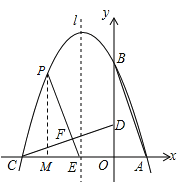
����CFE=90��ʱ����CFE�ס�COD������P��PM��x���ڵ�M������EFC�ס�EMP��
��![]() ��
��
��MP=3EM��
��P�ĺ�����Ϊt��
��P��t��-t2-2t+3����
��P�ڵڶ����ޣ�
��PM=-t2-2t+3��EM=-1-t��
��-t2-2t+3=-��t-1����t+3����
��ã�t1=-2��t2=-3����ΪP��C�غϣ�������ȥ����
��t=-2ʱ��y=-��-2��2-2����-2��+3=3��
��P��-2��3����
������CEF����COD����ʱ��P�������Ϊ����-1��4����-2��3����
����ֱ��CD�Ľ���ʽΪy=kx+b�������⣬��
![]() ��
��
��ã�![]() ��
��
��ֱ��CD�Ľ���ʽΪ��y=![]() x+1��
x+1��
��PM��CD�Ľ���ΪN�����N������Ϊ��t��![]() t+1����
t+1����
��NM=![]() t+1��
t+1��
��PN=PM-NM=-t2-2t+3-��![]() t+1��=-t2-
t+1��=-t2-![]() t+2��
t+2��
��S��PCD=S��PCN+S��PDN��
��S��PCD=![]() PN
PN![]() CM+
CM+![]() PN
PN![]() OM
OM
=![]() PN��CM+OM��
PN��CM+OM��
=![]() PN
PN![]() OC
OC
=![]() ��3��-t2-
��3��-t2-![]() t+2��
t+2��
=-![]() ��t+
��t+![]() ��2+
��2+![]() ��
��
����t=-![]() ʱ��S��PCD�����ֵΪ
ʱ��S��PCD�����ֵΪ![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�