题目内容
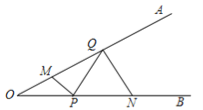
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=4,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是 .
【答案】![]() .
.
【解析】
试题分析:作M关于OB的对称点M',N关于OA的对称点N',连接两对称点M'N',交OB、OA于P、Q.此时MP+PQ+QN有最小值,根据线段垂直平分线性质和两点之间线段最短,MP+PQ+QN=M'P+PQ+QN'=M'N',M'N'的长度就是所求的MP+PQ+QN的最小值.分别连接OM',ON',∠N'OA=∠AOB=30°,∠M'OB=∠AOB=30°,所以∠M'ON'=90,所以三角形M'ON'是直角三角形,OM'=OM=1,ON'=ON=4,由勾股定理得M'N'为![]() .所以MP+PQ+QN的最小值是
.所以MP+PQ+QN的最小值是![]() .
.

练习册系列答案
相关题目