题目内容
【题目】如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,DE⊥AB于点E,连接CE交AD于点H,则图中的等腰三角形有( )
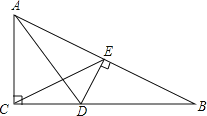
A.5个 B.4个 C.3个 D.2个
【答案】B
【解析】
试题分析:根据等腰三角形的判定,运用直角三角形的两个锐角互余和角平分线的性质,证得∠CAD=∠BAD=30°,
CD=ED,AC=AE,即△ABD、△CDE、△ACE、△BCE是等腰三角形
解:∵∠ACB=90°,∠B=30°,
∴∠BAC=60°,
∵AD是角平分线,
∴∠CAD=∠BAD=30°,
∴AD=BD.
∴△ABD是等腰三角形.
∵AD是角平分线,∠ACB=90°,DE⊥AB,
∴CD=ED
∴AC=AE
∴△CDE、△ACE是等腰三角形;
又△CEB也是等腰三角形
显然此图中有4个等腰三角形.
故选B.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目