题目内容
【题目】如图,在△ABC中,点E,F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,∠EAF=90°,BC=12,EF=5.
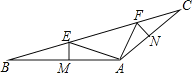
(1)求∠BAC的度数;
(2)求S△EAF.
【答案】(1)135°;(2)6
【解析】
试题分析:(1)先根据线段垂直平分线的性质得出∠B=∠BAE,∠C=∠CAF,再由三角形内角和定理得出∠BEA+∠CAF=45°,由∠BAC=∠BEA+∠EAF+∠CAF即可得出结论;
(2)先根据线段垂直平分线的性质得出EB=EA,FA=FC,根据EAFA的值即可得出结论.
解:(1)∵EM垂直平分AB,
∴∠B=∠BAE.
∵FN垂直平分AC,
∴∠C=∠CAF.
∵∠B+∠BAE+∠EAF+∠C+∠CAF=180°,∠EAF=90°,
∴2∠BEA+2∠CAF=90°,
∴∠BEA+∠CAF=45°,
∴∠BAC=∠BEA+∠EAF+∠CAF=45°+90°=135°;
(2)∵EM垂直平分AB,
∴EB=EA.
∵FN垂直平分AC,
∴FA=FC.
∵BC=12,EF=5,
∴EA+FA=12﹣5=7.
∵EF=5,∠EAF=90°,
∴EA2+FA2=(EA+FA)2﹣2EAFA=EF2=25,
∴![]() EAFA=6,
EAFA=6,
∴S△EAF=6.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目