Question

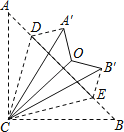
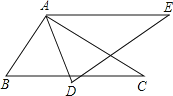
【题目】如图，△ABC≌△ADE，则，AB= ，∠E=∠ ．若∠BAE=120°，∠BAD=40°，则∠BAC= ．

Answer 1

【答案】AB、∠C、80°．

【解析】

试题分析：根据△ABC≌△ADE，可得其对应边对应角相等，即可得AB=AD，∠E=∠C，∠BAC=∠DAE；由∠DAC是公共角易证得∠BAD=∠CAE，已知∠BAE=120°，∠BAD=40°，即可求得∠BAC的度数．

解：∵△ABC≌△ADE，

∴AB=AD，∠E=∠C，∠BAC=∠DAE；

∵∠DAC是公共角

∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，

已知∠BAE=120°，∠BAD=40°，

∴∠CAE=40°，∠BAC=∠BAE﹣∠CAE=120°﹣40°=80°．

故答案分别填：AB、∠C、80°．