题目内容
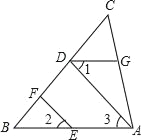
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)
【答案】见解析
【解析】试题分析:首先根据EF∥AD可得∠2=∠3,进而得到∠1=∠3,可判断出DG∥AB,然后根据两直线平行,同旁内角互补可得∠DGA+∠BAC=180°,进而得到答案.
试题解析:∵EF∥AD,(已知)
∴∠2=∠3(两直线平行同位角相等)
∵∠1=∠2,(已知)
∴∠1=∠3(等量代换)
∴DG∥BA,(内错角相等两直线平行)
∴∠AGD+∠CAB=180°,(两直线平行,同旁内角互补)
∵∠CAB=70°,(已知)
∴∠AGD=110°(等式性质).

练习册系列答案
相关题目