ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈ Χβ±≥ΨΑΘΚ ΐ―ßΜνΕ·ΩΈ…œάœ Π≥ω ΨΈ ΧβΘ§»γΆΦ1Θ§”–±Ώ≥ΛΈΣaΒΡ’ΐΖΫ–Έ÷ΫΤ§“Μ’≈Θ§»ΐ±Ώ≥ΛΖ÷±πΈΣaΓΔbΓΔcΒΡ»ΪΒ»÷±Ϋ«»ΐΫ«–Έ÷ΫΤ§ΝΫ’≈Θ§«“![]() Θ°«κΡψ”Ο’β»ΐ’≈÷ΫΤ§Τ¥≥ω“ΜΗωΆΦΑΗΘ§≤ΔΫΪ’βΗωΆΦΑΗΒΡΡ≥≤ΩΖ÷Ϋχ–––ΐΉΣΜρΤΫ“Τ±δΜΜ÷°ΚσΘ§Χα≥ω“ΜΗωΈ ΧβΘ®Ω…“‘ΧμΦ”ΤδΥϊΧθΦΰΘ§άΐ»γΩ…“‘Ηχ≥ωaΓΔbΒΡ÷Β»»ȩȰ
Θ°«κΡψ”Ο’β»ΐ’≈÷ΫΤ§Τ¥≥ω“ΜΗωΆΦΑΗΘ§≤ΔΫΪ’βΗωΆΦΑΗΒΡΡ≥≤ΩΖ÷Ϋχ–––ΐΉΣΜρΤΫ“Τ±δΜΜ÷°ΚσΘ§Χα≥ω“ΜΗωΈ ΧβΘ®Ω…“‘ΧμΦ”ΤδΥϊΧθΦΰΘ§άΐ»γΩ…“‘Ηχ≥ωaΓΔbΒΡ÷Β»»ȩȰ
ΫβΨωΈ ΧβΘΚ
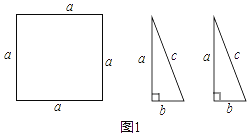
œ¬Οφ «ΝΫΗω―ßœΑ–ΓΉιΤ¥≥ωΆΦΑΗΚσΧα≥ωΒΡΈ ΧβΘ§«κΡψΫβΨωΥϊΟ«Χα≥ωΒΡΈ ΧβΘ°
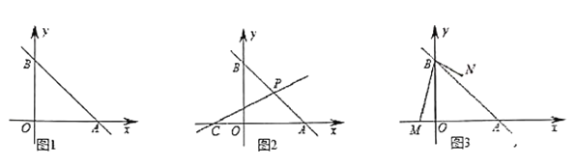
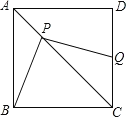
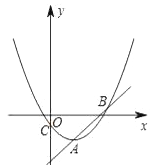
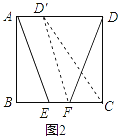
Θ®1Θ©ΓΑΑ°–ΡΓ±–ΓΉιΧα≥ωΒΡΈ Χβ «ΘΚ»γΆΦ2Θ§ΫΪΓςDFC»ΤΒψFΡφ ±’κ–ΐΉΣΘ§ ΙΒψD«ΓΚΟ¬δ‘ΎAD±Ώ…œΒΡΒψDΓδ¥ΠΘ§≤¬œκ¥Υ ±ΥΡ±Ώ–ΈAEFDΓδ « ≤Ο¥ΧΊ βΥΡ±Ώ–ΈΘ§≤ΔΦ”“‘÷ΛΟςΘΜ
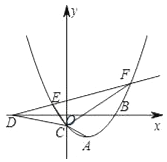
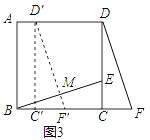
Θ®2Θ©ΓΑœΘΆϊΓ±–ΓΉιΧα≥ωΒΡΈ Χβ «ΘΚ»γΆΦ3Θ§ΒψMΈΣBE÷–ΒψΘ§ΫΪΓςDCFœρΉσΤΫ“Τ÷ΝDF«ΓΚΟΙΐΒψM ±ΆΘ÷ΙΘ§«“≤Ι≥δΧθΦΰa=6Θ§b=2Θ§«σΓςDCFΤΫ“ΤΒΡΨύάκΘ°
Ή‘÷ς¥¥–¬ΘΚ
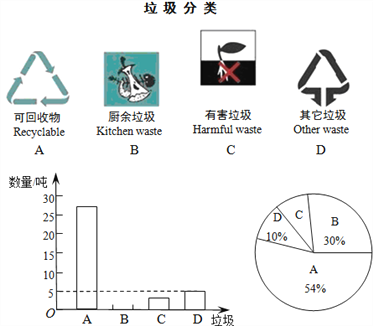
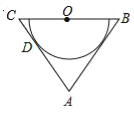
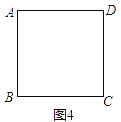
Θ®3Θ©«κΡψΖ¬’’…œ ω–ΓΉιΒΡΆ§―ßΘ§‘Ύœ¬ΟφΆΦ4ΒΡΩ’ΑΉ¥Π”Ο ΒœΏΜ≠≥ωΡψΤ¥≥ωΒΡΆΦΑΗΘ§”Ο–ιœΏΜ≠≥ω±δΜΜΆΦΘ§≤Δ‘ΎΚαœΏ¥Π–¥≥ωΡψΧα≥ωΒΡΈ ΧβΘ°Θ®≤Μ±ΊΫβ¥πΘ©
ΡψΧα≥ωΒΡΈ ΧβΘΚ________Θ°
ΓΨ¥πΑΗΓΩ![]() .
.
ΓΨΫβΈωΓΩ
ΡΘΖ¬Θ®1Θ©ΚΆΘ®2Θ©Χα≥ωΘΚΒ±a=6Θ§b=2 ±Θ§ΒψMΘ§NΖ÷±πΈΣADΘ§BC÷–ΒψΘ§ΫΪΓςMNF―ΊCBΖΫœρ“ΤΕ·Θ§ ΙΒψM¬δ‘ΎΒψA¥Π ±Θ§‘ΎAB…œΘ§AFΓδΫΜME”ΎGΘ§«σΓςGEFΒΡΟφΜΐΘ°
Θ®1Θ©÷ΛΟςΘΚΉςFGΓΆADΘ§
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§
ΓύΓœADC=ΓœC=90ΓψΘ§ADΓΈBCΘ§
ΓύΥΡ±Ώ–ΈGFCD «ΨΊ–ΈΘ§
ΓύGD=FC=bΘ§
ΓύFD=FDΓδΘ§
ΓύDΓδG=DG=bΘ§
ΓύADΓδ=AD©¹2DG=a©¹2bΘ§
ÿBE=FC=bȧ
ΓύEF=BC©¹2FC=a©¹2bΘ§
ΓύADΓδ=EFΘ§
ΓΏADΓδΓΈEFΘ§
ΓύΥΡ±Ώ–ΈAEFDΓδ «ΤΫ––ΥΡ±Ώ–Έ
Θ®2Θ©ΫβΘΚ”…ΤΫ“Τ÷ΣΘ§ΓœCΓδDΓδFΓδ=ΓœCDF=ΓœEBCΘ§
ΓΏΓœCΓδDΓδFΓδ+ΓœBFΓδM=90ΓψΘ§
ΓύΓœMBFΓδ+ΓœBFΓδM=90ΓψΘ§
ΓύΓœBMFΓδ=90ΓψΘ§
”…Ι¥Ι…Ε®άμΒΟΘ§BE=![]() =2
=2![]() Θ§
Θ§
ΓΏΒψMΈΣBE÷–ΒψΘ§
ΓύBM=![]() Θ§
Θ§
ΓΏΓœBMFΓδ=ΓœBCEΘ§ΓœMBFΓδ=ΓœCBEΘ§
ΓύΓςBMFΓδΓΉΓςBCEΘ§
Γύ ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύBFΓδ=![]() Θ§
Θ§
ΓΏBF=BC+CF=8Θ§
ΓύFΓδF=BF©¹BFΓδ=![]() Θ§
Θ§
ΓύΓςDCFΤΫ“ΤΒΟΨύάκΈΣ![]() ΘΜ
ΘΜ
Θ®3Θ©Χα≥ωΒΡΈ ΧβΘΚ
Β±a=6Θ§b=2 ±Θ§ΒψMΘ§NΖ÷±πΈΣADΘ§BC÷–ΒψΘ§ΫΪΓςMNF―ΊCBΖΫœρ“ΤΕ·Θ§ ΙΒψM¬δ‘ΎΒψA¥Π ±Θ§‘ΎAB…œΘ§AFΓδΫΜME”ΎGΘ§«σΓςGEFΒΡΟφΜΐΘ°
»γΆΦΘ§
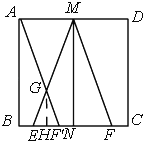
ΓΏMN=BC=b=6Θ§NF=BFΓδ=a=2Θ§
ΓύFC=BE=FΓδN=1Θ§
ΓύEFΓδ=1Θ§
ΓύEH=FΓδH=![]() EFΓδ=
EFΓδ=![]() Θ§
Θ§
ÿGHøABȧ
Γύ![]()
Γύ![]() Θ§
Θ§
ΓύGH=![]() Θ§
Θ§
ΓύSΓςGEFΓδ=![]() ΓΝEFΓδΓΝGH=
ΓΝEFΓδΓΝGH=![]() .
.

 ΨΪ”ΔΩΎΥψΩ®œΒΝ–¥πΑΗ
ΨΪ”ΔΩΎΥψΩ®œΒΝ–¥πΑΗ ”Π”ΟΧβΒψ≤ΠœΒΝ–¥πΑΗ
”Π”ΟΧβΒψ≤ΠœΒΝ–¥πΑΗ