题目内容
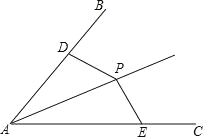
【题目】已知:在正方形ABCD中,AB=3,E是边BC上一个动点(点E不与点B,点C重合),连接AE,点H是BC延长线上一点.过点B作BF⊥AE,交AE于点G,交DC于点F.
(1)求证:AE=BF;
(2)过点E作EM⊥AE,交∠DCH的平分线于点M,连接FM,判断四边形BFME的形状,并说明理由;
(3)在(2)的条件下,∠EMC的正弦值为![]() ,求四边形AGFD的面积.
,求四边形AGFD的面积.
【答案】(1)见解析;(2)四边形BFME是平行四边形,见解析;(3)S四边形ADFG=![]() .
.
【解析】
(1)结合正方形的性质证△ABE≌△BCF即可;
(2)要证四边形BFME是平行四边形,由(1)知△ABE≌△BCF(ASA)且AE=BF,若能证AE=EM,则BF=EM,只需再证BF∥EM即可,因此为证AE=EM,可构造以AE为边的三角形使其与△ECM全等,可在AB上截取BN=BE,构造三角形AEN,进行证明即可;
(3)如图2,连接BD,过点F作FN⊥BD于点N,由正方形、平行线及角平分线的性质可知∠EMC=∠DBF,所以sin∠EMC=sin∠DBF=![]() =
=![]() ,设NF=
,设NF=![]() a,BF=10a,由正方形的性质,可知BD,ND长,BN=BD-ND,在直角三角形BNF中BF2﹣NF2=BN2,据此求出a的值,即知NF,BF长,同样,DF,FC,BE,EC的长也能求出,再由△BGE∽△BCF求出 BG,GE长,此时,可求出四边形ADEC,ECFG的面积,作差即得四边形AGFD的面积.
a,BF=10a,由正方形的性质,可知BD,ND长,BN=BD-ND,在直角三角形BNF中BF2﹣NF2=BN2,据此求出a的值,即知NF,BF长,同样,DF,FC,BE,EC的长也能求出,再由△BGE∽△BCF求出 BG,GE长,此时,可求出四边形ADEC,ECFG的面积,作差即得四边形AGFD的面积.
解:证明:(1)∵在正方形ABCD中,
∴∠ABE=∠BCF=90°,AB=BC,
∵∠BAE+∠ABF=90°,∠CBF+∠ABF=90°,
∴∠BAE=∠CBF,且∠ABE=∠BCF=90°,AB=BC,
∴△ABE≌△BCF(ASA)
∴AE=BF,
(2)四边形BFME是平行四边形
理由如下:如图1:在AB上截取BN=BE,

∵△ABE≌△BCF
∴∠BAE=∠FBC
∵AB=BC,BN=BE,
∴AN=EC,∠BNE=45°
∴∠ANE=135°
∵CM平分∠DCH
∴∠DCM=∠MCH=45°
∴∠ECM=135°=∠ANE
∵AE⊥EM
∴∠AEB+∠MEC=90°,∠AEB+∠BAE=90°
∴∠BAE=∠MEC,且AN=EC,∠ANE=∠DCM
∴△ANE≌△ECM(SAS)
∴AE=EM,∠BAE=∠MEC
∴∠BAE=∠FBC=∠MEC
∴BF∥EM,且BF=AE=EM
∴四边形BFME是平行四边形
(3)如图2,连接BD,过点F作FN⊥BD于点N,

∵四边形ABCD是正方形,
∴AB=BC=CD=3,∠DBC=∠BDC=45°,
∴BD=3![]() ,∠DBF+∠FBC=45°
,∠DBF+∠FBC=45°
∵∠MCH=∠MEC+∠EMC=45°,∠FBC=∠MEC
∴∠EMC=∠DBF
∴sin∠EMC=sin∠DBF=![]() =
=![]()
∴设NF=![]() a,BF=10a,
a,BF=10a,
∵∠BDC=45°,FN⊥BD
∴DN=NF=![]() a,DF=
a,DF=![]() NF=2a
NF=2a
∴BN=3![]() ﹣
﹣![]() a
a
∵BF2﹣NF2=BN2,
∴98a2=(3![]() ﹣
﹣![]() a)2,
a)2,
∴a=![]()
∴DF=2×![]() =
=![]()
∴FC=![]()
∵△ABE≌△BCF
∴BE=CF=![]() ,
,
∴EC=![]() ,BF=
,BF=![]() =
=![]()
∵∠FBC=∠FBC,∠BGE=∠BCF
∴△BGE∽△BCF
∴![]()
∴
∴BG=![]() ,GE=
,GE=![]()
∴S四边形ADFG=S四边形ADEC﹣S四边形ECFG,
∴S四边形ADFG=![]()

 计算高手系列答案
计算高手系列答案【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?