题目内容
【题目】二次函数y=x2+bx﹣t的对称轴为x=2.若关于x的一元二次方程x2+bx﹣t=0在﹣1<x<3的范围内有实数解,则t的取值范围是( )
A. ﹣4≤t<5B. ﹣4≤t<﹣3C. t≥﹣4D. ﹣3<t<5
【答案】A
【解析】
根据抛物线对称轴公式可先求出b的值,一元二次方程x2+bx﹣t=0在﹣1<x<3的范围内有实数解相当于y=x2﹣bx与直线y=t的在﹣1<x<3的范围内有交点,即直线y=t应介于过y=x2﹣bx在﹣1<x<3的范围内的最大值与最小值的直线之间,由此可确定t的取值范围.
解:∵抛物线的对称轴x=![]() =2,
=2,
∴b=﹣4,
则方程x2+bx﹣t=0,即x2﹣4x﹣t=0的解相当于y=x2﹣4x与直线y=t的交点的横坐标,
∵方程x2+bx﹣t=0在﹣1<x<3的范围内有实数解,
∴当x=﹣1时,y=1+4=5,
当x=3时,y=9﹣12=﹣3,
又∵y=x2﹣4x=(x﹣2)2﹣4,
∴当﹣4≤t<5时,在﹣1<x<3的范围内有解.
∴t的取值范围是﹣4≤t<5,
故选:A.

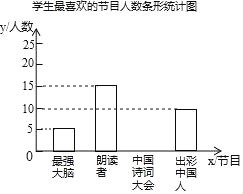
【题目】为了解某校中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:根据以上提供的信息,解答下列问题:
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
(1)x= ,a= ,b= ;
(2)补全上面的条形统计图;
(3)在喜爱《最强大脑》的学生中,有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加潍坊市组织的竞赛活动,请用树状图或列表法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
【题目】“倡导全民阅读”“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.某中学在全校学生中随机抽取了部分学生对2018年度阅读情况进行问卷调查,并将收集的数据统计如表
数量/本 | 15 | 11 | 8 | 4 | 3 | 2 |
人数 | 80 | 60 | 50 | 100 | 40 | 70 |
根据表中的信息判断,下列结论错误的是( )
A. 该校参与调查的学生人数为400人
B. 该校学生2018年度阅读书数量的中位数为4本
C. 该校学生2018年度阅读书数量的众数为4本
D. 该校学生2018年平均每人阅读8本书