题目内容
【题目】如图,在长方形ABCD中,AB=6,AD=8,沿BD折叠使点A到点A′处,DA′交BC于点F.
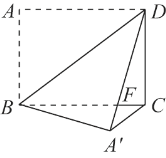
(1)求证:FB=FD;
(2)求证:CA′∥BD;
(3)求△DBF的面积.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据折叠的性质和矩形的性质可得∠ADB=∠BDA′,∠ADB=∠DBC,等量代换求出∠BDA′=∠DBC,然后根据等角对等边可得结论;
(2)首先求出FC=FA′,得到∠FCA′=∠FA′C,然后根据∠BFD=∠CFA′求出∠FBD=∠FCA′,利用平行线的判定可得结论;
(3)设FB=FD=x,则A′F=8-x,在Rt△BA′F中,利用勾股定理构造方程求出BF即可解决问题.
解:(1)由折叠的性质可得:∠ADB=∠BDA′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠BDA′=∠DBC,
∴FB=FD;
(2)由折叠的性质可得:AD=A′D,
∵四边形ABCD是矩形,
∴AD=BC,
∴A′D=BC,
∵FB=FD,
∴FC=FA′,
∴∠FCA′=∠FA′C,
∵∠BFD=∠CFA′,
∴∠FBD+∠FDB=∠FCA′+∠FA′C,即2∠FBD=2∠FCA′,
∴∠FBD=∠FCA′,
∴CA′∥BD;
(3)∵AD=A′D=8,AB=A′B=6,FB=FD,∠BA′F=∠A=90°,
∴设FB=FD=x,则A′F=8-x,
在Rt△BA′F中,∵BA′2+A′F2=BF2,
∴![]() ,
,
解得:![]() ,即
,即![]() ,
,
∴![]() .
.

练习册系列答案
相关题目