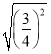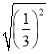题目内容
【题目】先阅读下题的解答过程,然后解答后面的问题,
已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值
解法一:设2x3﹣x2+m=x+m=(2x+1)(x2+ax+b)
则2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得 ,解得
,解得 ∴m=
∴m=![]() .
.
解法二:设2x3﹣x2+m=A(2x+1)(A为整式)
由于上式为恒等式,为方便计算取x=![]() ,
,![]() ,故m=
,故m=![]()
选择恰当的方法解答下列各题
(1)已知关于的多项式x2+mx﹣15有一个因式是x﹣3,m= .
(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值:
(3)已知x2+2x+1是多项式x3﹣x2+ax+b的一个因式,求a,b的值,并将该多项式分解因式.
【答案】(1)2;(2)m=﹣5,n=20;(3)a=﹣5,b=﹣3,该多项式分解因式为:x3﹣x2﹣5x﹣3=(x﹣3)(x+1)2
【解析】
(1)根据多项式乘法将等式右边展开有:x2+mx﹣15=(x﹣3)(x+n)=x2+(n﹣1)x﹣n,所以,根据等式两边对应项的系数相等可以求得m的值;
(2)设x4+mx3+nx﹣16=A(x﹣1)(x﹣2)(A为整式),分别取x=1和x=2得关于m和n的二元一次方程组,求解即可;
(3)设x3﹣x2+ax+b=(x+p)(x2+2x+1),将等式右边展开,比较系数,得关于p,a,b的三元一次方程组,解方程组,再进行因式分解即可.
解:(1)由题设知:x2+mx﹣15=(x﹣3)(x+n)=x2+(n﹣3)x﹣3n,
故m=n﹣3,﹣3n=﹣15,
解得n=5,m=2.
故答案为:2;
(2)设x4+mx3+nx﹣16=A(x﹣1)(x﹣2)(A为整式),
分别令x=1和x=2得:
![]() ,
,
解得:![]() ,
,
∴m=﹣5,n=20;
(3)设x3﹣x2+ax+b=(x+p)(x2+2x+1),
∵(x+p)(x2+2x+1)
=x3+(2+p)x2+(1+2p)x+p,
∴ ,
,
解得: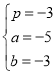 ,
,
∴多项式x3﹣x2+ax+b=x3﹣x2﹣5x﹣3,
∴x3﹣x2﹣5x﹣3
=(x﹣3)(x2+2x+1)
=(x﹣3)(x+1)2,
∴a=﹣5,b=﹣3,该多项式分解因式为:x3﹣x2﹣5x﹣3=(x﹣3)(x+1)2.