题目内容
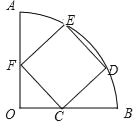
【题目】如图,在圆心角为90°的扇形OAB中,点F、C在半径OA、OB上,且OC=OF,以CF为边作正方形CDEF,另两顶点D、E在弧AB上,若扇形OAB的面积为25π,则正方形CDEF的面积为( )
A. 25 B. 40 C. 50 D. ![]() π
π
【答案】B
【解析】
作OH⊥DE于H,交CF于G,连接OD,则DH=EH,先利用扇形的面积公式计算出OD=10,设正方形CDEF的边长为x,证明△OCF为等腰直角三角形得到OG=![]() CF=
CF=![]() x,利用四边形CGHD为矩形得到GH=CD=x,则OH=
x,利用四边形CGHD为矩形得到GH=CD=x,则OH=![]() x,然后根据勾股定理得到(
x,然后根据勾股定理得到(![]() x)2+(
x)2+(![]() x)2=102,则求出x2即可得到正方形CDEF的面积.
x)2=102,则求出x2即可得到正方形CDEF的面积.
作OH⊥DE于H,交CF于G,连接OD,则DH=EH,

设扇形OAB的半径为r,则![]() =25π,解得r=10,
=25π,解得r=10,
即OD=10,
设正方形CDEF的边长为x,
∵CF∥DE,
∴OG⊥CF,
∵OC=OF,
∴△OCF为等腰直角三角形,
∴OG=![]() CF=
CF=![]() x,
x,
易得四边形CGHD为矩形,
∴GH=CD=x,
∴OH=![]() x,
x,
在Rt△ODH中,(![]() x)2+(
x)2+(![]() x)2=102,
x)2=102,
∴x2=40,
∴正方形CDEF的面积为40.
故选B.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目